Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 58
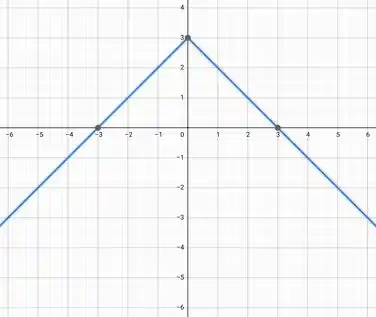
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico.
Passo 1
Podemos definir o domínio como , ou seja, os valores de x que fazem a função existir. Já a imagem é formada pelos valores de y que pertencem à função, ou seja, .
Passo 2
Como não há valores de x que fazem a função não existir,
Passo 3
Assim,
Passo 4
E para construir o gráfico, basta fazer o gráfico do módulo, rebater para baixo por causa do sinal de menos e somar (subir) três unidades.
Resposta
Exercícios de Livros Relacionados
Dada a função f x = x - 2 x , calcular f ( - 1 ) , f - 1 2ef - 2 3 . Mostrar que f ( a ) = - | a | .
Determine o domínio das funções. y = x 2 - 4 x + 3
Se f x = 3 x - 1 x - 7 , determine:d) f t + f 4 t
Seja f ( n ) a soma dos n termos de uma progressão aritmética. Demonstrar que f n + 3 - 3 f n + 2 + 3 f n + 1 - f n = 0 .
Seja f x = x - 2 8 - x para 2 ≤ x ≤ 8 . Determinar f 5 ,f - 1 2 ef 1 2 . Qual o domínio da função f x ? Determinar f 1 - 2 t e indicar o domínio.Determinar f f 3 ef f 5 . Traçar o gráfico de f x .