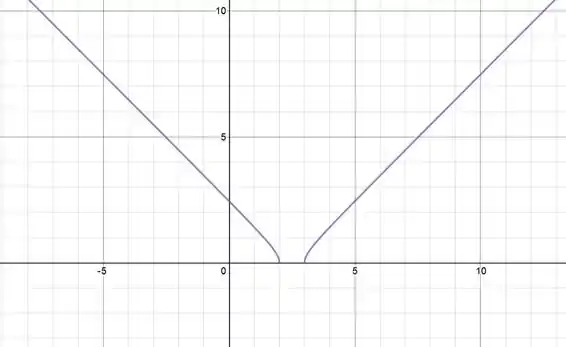
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Vamos determinar uma técnica para determinar o domínio e a imagem dessa função. Lembra de como fatoramos os polinômios do 2º grau nos últimos exercícios? Vamos usar a mesma lógica! Lembre-se que:
Onde e são as raízes do polinômio.
Vamos nos aproveitar do fato de que precisamos que o que está dentro da raiz seja positivo ou , e também sabemos que para uma multiplicação entre números ser positiva, precisamos que os dois tenham o mesmo sinal. Ou seja:
Se os dois forem negativos, o produto também vai ser positivo como precisamos:
Então só vamos considerar esses dois casos. Os casos para os quais e têm sinais diferentes serão desconsiderados, já que isso não satisfaria a condição da raiz. Repare que os nossos intervalos de análise são fechados, pois o argumento da raiz também pode ser .
Passo 2
A equação do 2º grau que queremos determinar as raízes é:
Por bhaskara:
E daí temos nossas duas raízes:
E
Passo 3
Então podemos reescrever a função:
como:
E agora vamos fazer aquelas duas condições para encontrar o nosso domínio. Começando com ambos os termos positivos:
Para satisfazer as duas proposições precisamos que:
Daí já temos que faz parte do nosso domínio.
Agora vamos considerar o outro caso:
E para satisfazer as duas condições:
Agora vamos unir esse intervalo ao outro e teremos o nosso domínio!
Passo 4
A imagem será para todos os positivos, como se fosse uma simples função .
Passo 5
A partir dos pontos da nossa imagem e do nosso domínio, sabemos a partir de onde a nossa função sobe do eixo : e . Esses serão os mínimos da nossa função. Daí a nossa função vai dar uma subida e depois se estabilizar como uma reta. Isso acontece porque temos uma função quadrática dentro de uma raiz quadrada, que são funções inversas e quando uma função inversa dentro da outra, ficamos com , que é a uma reta!
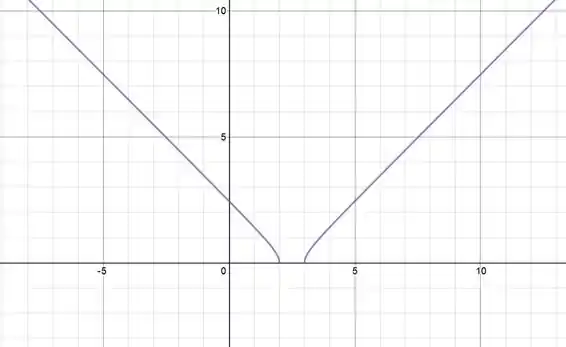
Resposta
Domínio:
Imagem: