Dados os gráficos de e :
(a) Obtenha os valores de e .
(b) para quais valores de ?
(c) Estime a solução da equação .
(d) Em qual intervalo é decrescente?
(e) Dê o domínio e a imagem de .
(f) Obtenha o domínio e a imagem de .
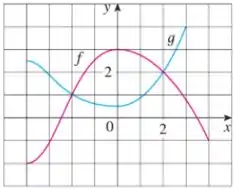
Passo 1
Falaee, belezinha?

Bom... A questão nos dá o esboço de duas funções e :
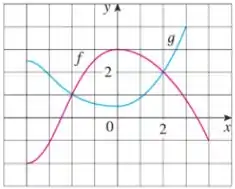
A partir disso, temos várias questõezinhas sobre essa plotagem.
Vamos combinar o seguinte... à medida que vamos fazendo uma a uma, eu vou te explicando porque se eu falar tudo de uma vez sobre o que vamos fazer vai ficar beem bagunçado haha.
Combinado assim?? Então bora lá!! 😉
Mas antes... essa questão serve para que tenhamos uma noção inicial (e fundamental!) sobre como analisar duas funções de um ponto de vista gráfico.
Tudo que a gente precisa fazer é analisar a a figura e extrair as informações pedidas, então bora lá!!
Passo 2
Na letra a) queremos encontrar e .
Em outras palavras, queremos o valor de quando e o valor de quando .
Vamos riscar um pouquinho o gráfico e analisar os valores correspondentes (sabendo que cada lado de um quadradinho vale 1 unidade):
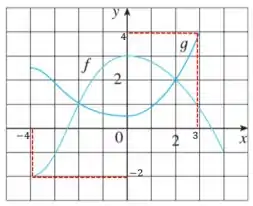
Assim, podemos concluir que:
Tranquilo até aqui? 😇
Passo 3
(b) Para , então só precisamos ver onde os gráficos de e de se tocam.
Nesses pontos, verificamos qual o valor de e teremos a resposta!
Analisando a plotagem, temos:
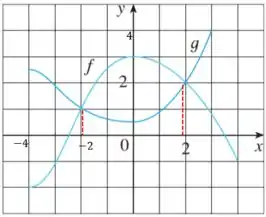
Assim, concluímos que para e .
Legal, né? 😐
Passo 4
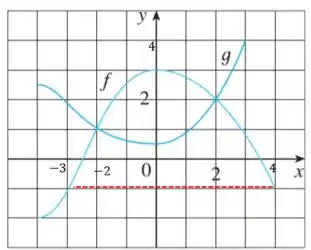
(c) O que queremos saber aqui é qual o valor de que faz com que seja igual à .Precisamos lembrar que os valores assumidos por são representados no eixo , beleza?
Então a gente tem que ver onde, no gráfico de , temos um , e aí vemos o valor de correspondente.
Nesse caso, teremos que e que , veja:
Bora continuar! 😉
Passo 5
(d) Aqui é só a gente ver no gráfico de onde os valores de diminuem conforme os valores de aumentam.
Com isso na cabeça, dá pra ver que o intervalo que a gente quer vai de até .
Em notação um pouquinho formal, podemos representar esse intervalo como sendo .
Estamos quase lá! 👀
Passo 6
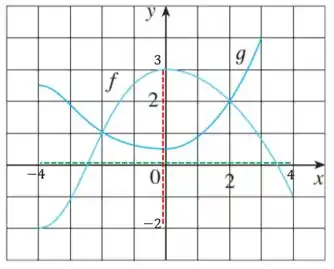
(e) O domínio de vão ser todos os valores de que estão presente no gráfico de , enquanto a imagem é referente aos valores em do gráfico.
O domínio (em verde) vai ser o conjunto de valores que vão de até , ou seja, o intervalo .
Enquanto isso, a imagem (em vermelho) vai ser o intervalo de .
Fechou? ;)
Passo 7
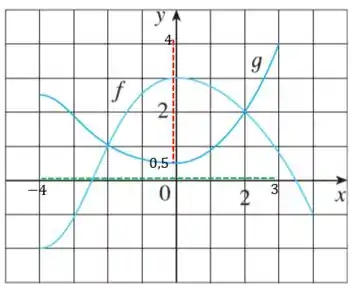
(f) Essa aqui é a mesma coisa da letra (e), mas agora a gente vai analisar o gráfico de .
Partindo da mesma ideia, temos que o domínio (em verde) de vai ser o intervalo , enquanto a imagem (em vermelho) será o intervalo :
E aí! entendeu tudo? Responde Aí! 😁
Resposta
- e .
- para e .
- para e .
- é decrescente no intervalo .
- O domínio de é o intervalo e a imagem o intervalo .
- O domínio de é o intervalo e a imagem o intervalo .