Nesta seção discutimos exemplos de funções cotidianas: a população em função do tempo; o custo da franquia postal em função do peso; a temperatura da água em função do tempo. Dê três novos exemplos de funções cotidianas que possam ser descritas verbalmente. O que você pode dizer sobre o domínio e a imagem de cada uma dessas funções? Se possível, esboce um gráfico para cada uma delas.
Passo 1
Eaeee, belezinha??

A questão nos pede para fornecermos três exemplos de funções cotidianas que possam ser descritas verbalmente. Isso significa que nós devemos pensar em situações comuns do dia a dia que possam ser modeladas por uma relação matemática, onde uma variável depende de outra. Por exemplo, a temperatura de um objeto em função do tempo, ou o preço de um produto em função da quantidade vendida, são exemplos de funções cotidianas.
Além disso, a questão também nos pede para discutirmos o domínio e a imagem de cada uma dessas funções. O domínio é o conjunto de todos os possíveis valores de entrada da função, enquanto a imagem é o conjunto de todos os possíveis valores de saída. Por exemplo, se estivermos falando sobre a temperatura de um objeto em função do tempo, o domínio pode ser todos os valores de tempo (por exemplo, horas do dia) e a imagem pode ser todos os valores de temperatura possíveis (por exemplo, graus Celsius).
Por fim, se possível, a questão nos sugere que desenhemos um gráfico para cada uma das funções. Isso pode nos ajudar a visualizar como as variáveis estão relacionadas e como a função se comporta ao longo de diferentes valores do domínio.
Resumindo, nós devemos dar exemplos de situações cotidianas que podem ser modeladas por funções matemáticas, explicar quais são os valores possíveis de entrada e saída para cada exemplo e, se possível, desenhar um gráfico que represente essa relação.
Passo 2
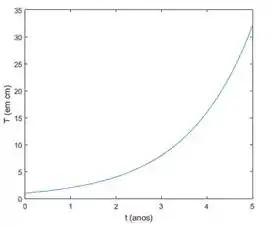
Exemplo : Podemos pensar em um determinado tumor de tamanho , em centímetros, que depende do tempo em anos. Vamos considerar que esse tumor tem um tamanho inicial de e dobra a cada ano, por exemplo;
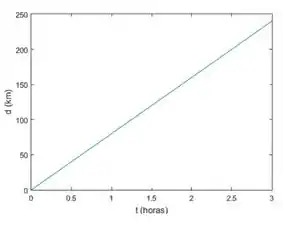
Exemplo : Um carro percorre uma distância , em quilômetros, em função do tempo , em horas. Aqui vamos considerar que o carro tinha uma velocidade de uns e viajou por um tempo de horas;
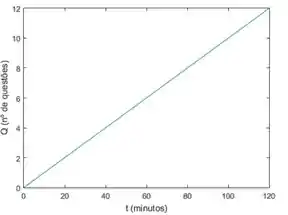
Exemplo : Um estudante de engenharia tem que estudar para uma prova de cálculo e decide resolver umas questões no Responde Aí para se preparar. O número de questões que ele consegue resolver estão em função do tempo , em minutos. Digamos que ele consegue resolver questão a cada minutos e decide estudar por horas (120 minutos), resolvendo questões.
Legal, né? 😉
Passo 3
Bom, agora a gente vai analisar o domínio e imagem de cada função.
O domínio ta sempre relacionado à variável independente, aquela que “dita a regra” da função (no nosso caso, temos o tempo como variável independente em todos os exemplos).
A imagem ta relacionada à variável dependente, que no nosso caso é o tamanho , a distância e o número de questões .
Entendido? Bora verificar cada exemplo agora:
Passo 4
Exemplo : A gente sabe que o tempo pode ir de um instante inicial () até o infinito. Dessa forma, o dominío da função é o intervalo .
No exemplo, o tamanho do tumor começa em e cresce até um tamanho indefinido.
A gente pode dizer então que a imagem da função vai ser ;
Aqui a nossa função vai ser .
O gráfico na figura vai até , mas temos que lembrar que, mesmo assim, a função vai até o infinito, combinado?
Tranquilo até aqui? 😬
Passo 5
Exemplo : Aqui o tempo foi delimitado, diferente do exemplo anterior.
Como o carro viajou durante um período de horas, o domínio da função será .
Como o carro estava se movendo a uma velocidade de , a máxima distância percorrida por ele será de .
A imagem dessa função então vai ser o intervalo .
Essa aqui vai ser uma reta dada por .
Aqui a gente já vê que o gráfico ta dentro dos intervalos que achamos (a função não existe fora deles, fica atento nisso!)
Sacou?
Passo 6
Exemplo : Esse caso é beeem parecido com o caso anterior, mas em outro contexto.
De cara dá pra ver que a função vai ter o domínio no intervalo e a imagem no intervalo
Ta acabando! Essa é a nossa última função.
Como o problema é parecido com o anterior, a gente também vai ter uma reta, mas essa aqui vai ser dada por .
Dá uma olhada em como fica o gráfico:
Pronto! A gente acabou a análise pedida na questão.
Deu um trabalhinho, mas é só fazer com calma! ;)
O que achou? Responde Aí! 😐
Resposta
Respostas no passo a passo.