Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.6 - Ex. 33
Determine a equação do plano tangente à superfície parametrizada dada no ponto especificado. Se você tiver um programa que trace o gráfico de superfícies parametrizadas, use-o para traçar a superfície e o plano tangente.
Passo 1
E aê, galerinha legal! 😊
Precisamos encontrar a equação do plano tangente à superfície parametrizada dada por
Depois, podemos fazer um gráfico dessas superfícies.
Lembrem-se de que, para determinar a equação do plano, é preciso um ponto que pertence a ele e um vetor normal ? A equação do plano é:
Quando falamos em plano tangente à superfície o vetor normal é dado pelo produto vetorial dos vetores e que são as derivadas parciais da função paramétrica em relação às variáveis e de parametrização.
O ponto já foi dado. É e , nas coordenadas cartesianas:
Assim
Passo 2
Agora temos que encontrar o vetor normal ao plano. Vamos montar a função vetorial:
Agora vamos fazer a derivada parcial de em relação à :
Agora vamos fazer a derivada parcial de em relação à :
E agora calcular o vetor normal ao plano :
Assim o vetor normal ao plano é .
Passo 3
Já que temos o vetor normal e o ponto , e lembrando que a equação do plano é (dá uma espiada no passo um):
Agora é só substituir!
Podemos simplificar a equação dividindo todos os termos por
Graficamente, teríamos
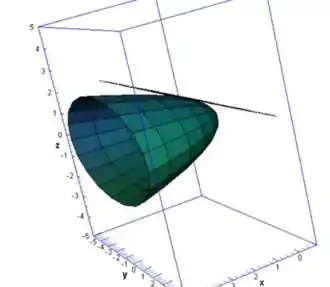
Show de bola! 😉