Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.6 - Ex. 3

Identifique a superfície que tem a equação paramétrica dada.

r → x , θ = x , cos ⁡ θ ,   s e n   θ

Passo 1

Olá, tudo bem? Vamos ver o que a questão quer

Ela pede para a gente achar a superfície que tem a equação paramétrica

r → x , θ = x , cos ⁡ θ ,   s e n   θ

Só isso 😅

Lembrando que essa equação é um vetor da forma

x , y , z

Ok?

Então, vamos identificar cada coordenada e tentar converter todas para as coordenadas cartesianas x , y , z , pois fica mais fácil de identificar a superfície. Depois farei um esboço dele.

Bora lá?

Passo 2

Vamos identificar cada coordenada da equação

r → x , θ = x , cos ⁡ θ ,   s e n   θ

Temos que

x = x y = c o s θ z = s e n θ

Queremos eliminar aqueles cossenos e senos, então vamos elevar eles ao quadrado para podermos utilizar propriedade trigonométrica

sen 2 ⁡ θ + cos 2 ⁡ θ = 1

E assim, sumir com eles!

Fazendo y 2

y 2 = cos 2 ⁡ θ

Fazendo z 2

z 2 = s e n 2 θ

Muito bem! Mas as coordenadas estão separadas, não podemos usar a propriedade. Vamos somar elas então!

Temos

y 2 + z 2

Que é a mesma coisa que

y 2 + z 2 = s e n 2 θ + cos 2 ⁡ θ

y 2 + z 2 = 1

Assim em termos de z e y teremos a equação de um círculo de raio 1 :

y 2 + z 2 = 1

Passo 3

Excelente! E a parte em x ? 🙄

Bom, lembra que em superfícies, quando uma variável não aparece é porque temos simetria em relação a ela?

Como x não aparece em

y 2 + z 2 = 1

Temos um cilindro circular reto de raio 1 ao longo do eixo x .

Assim:

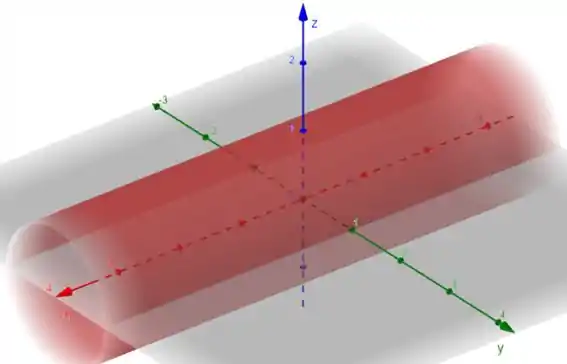
Tranquilo?

Resposta

c i l i n d r o   c i r c u l a r   r e t o   a o   l o n g o   d e   x

y 2 + z 2 = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça uma correspondência entre as equações e os gráficos identificados por I - V I e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. r u ,
Identifique a superfície que tem a equação paramétrica dada. r x , θ = x , x cos ⁡ θ , x sen ⁡ θ
Faça uma correspondência entre as equações e os gráficos identificados por I-VI e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. r u , v
Faça uma correspondência entre as equações e os gráficos identificados por I - V I e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. r u ,
Faça uma correspondência entre as equações e os gráficos identificados por I - V I e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. x = 1