Determine e esboce o domínio da função . Qual é a imagem de
?
Passo 1
Olá, meu brother. Vamos resolver essa atividade hoje.
Queremos determinar o domínio de . Ou seja, queremos saber que valores de podem ser usados para que seja real.
Para definir o domínio, basta olhar para as restrições das funções. No nosso caso, temos uma função raiz quadrada, e não podemos ter números negativos dentro da raiz. Então iremos descobrir o conjunto de valores para que:
Já a imagem de uma função, é o conjunto de valores possíveis para a função, você deve se perguntar, qual o conjunto de valores que minha função pode ter?
Passo 2
Então temos a nossa função:
Logo, como está dentro da raiz,
Olhando para a parábola , vemos que (o domínio) é representado pela área hachurada na figura. Qualquer ponto dessa área faz parte do domínio.
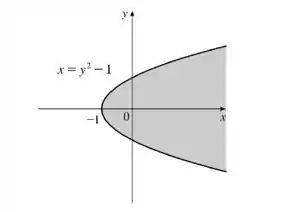
Assim, o domínio é definido por
Passo 3
Queremos determinar a imagem de . Ou seja, se usarmos todas as combinações possíveis de valores do domínio, quais serão todos os valores possíveis de ?
Assim como fizemos para o domínio, vamos dar uma olhada nas restrições.
Logo, a imagem de está no intervalo .
Resposta
O domínio é definido por
A imagem de está no intervalo .