- Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescente
- Identifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem
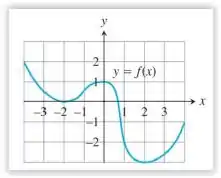
Passo 1
Observando a imagem tem que a função cresce nos intervalos e decresce em
Assim, temos como máximo absoluto o ponto e mínimo absoluto
E seus máximos locais os pontos e . Já seu mínimo local é o ponto
Resposta
A função cresce nos intervalos e decresce em
Máximo absoluto o ponto e mínimo absoluto
E seus máximos locais os pontos e . Já seu mínimo local é o ponto