Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 6
Determine uma janela retangular apropriada para a função dada e use-a para fazer gráfico da função.
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão da pra gente a função:
E pede pra gente determinar uma janela retangular apropriada para ela, e também pede pra gente fazer o gráfico dessa função.
E para que possamos fazer isso, o caminho é entender direitinho onde a função está definida. Ou seja, vamos analisar seu domínio. Além disso, vamos estudar seu comportamento de acordo com as variações de . Assim poderemos ver a melhor janela como sendo aquela em que o comportamento da função fica melhor representado.
Vem comigo que te ajudo melhor com isso nos próximos passos.
Passo 2
Para determinar a melhor janela, vamos primeiro analisar o domínio da função, certo?
Sendo
Uma função onde temos uma expressão dentro de uma raiz quadrada, teremos um probleminha. Essa função não está definida quando o que está dentro da raiz é negativo. Ou seja, precisamos que
Ou seja,
Então os valores de que são interessantes para a nossa janela são , já que valores de fora desse intervalo não estarão representados na função.
Como
E a largura da janela pode ser de .
Passo 3
Um outro ponto importante a ser mostrado seria onde a função corta em ou seja, para E isso acontece em:
Além disso, a imagem e formada apenas valores maiores ou iguais a zero, já que a raiz quadrada nunca será negativa.
Assim, a altura da nossa janela pode estar de
Passo 4
Juntando tudo que vimos até aqui, temos a janela escolhida como sendo:
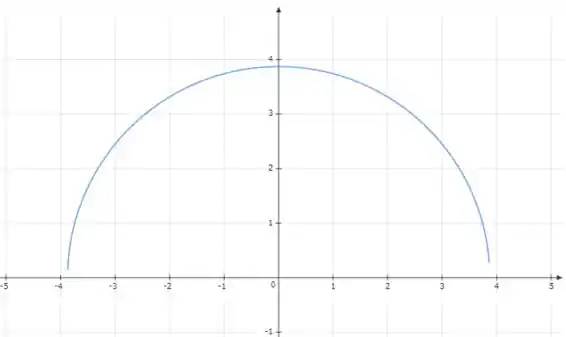
Resposta
Uma janela apropriada é:
