Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 4
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Falaaaaaa aí, belezinha??
Bom... a questão nos pede para determinar uma janela retangular apropriada para a funç��o
E use-a para fazer o gráfico da função.
Mas que janela é essa??
Então... quando a gente olha um gráfico, a gente quer tirar todas as informações que estão contidas nele. E, para isso, o gráfico não pode estar nem grande demais para o plano cartesiano e nem pequeno demais.
O tamanho ideal é aquele que contém o máximo de informações possíveis que podemos extrair do gráfico.
Para isso, precisamos calcular pontos chaves que nos dirão o tamanho correto da janela.
E aí? Bora lá??
Passo 2
Da nossa função, temos:
De cara, já vemos que é uma das raízes, pois:
Agora, vamos encontrar os pontos de máximo e mínimo da nossa expressão (já que temos uma função de grau ):
Derivando pelo método de derivação polinomial, temos:
Calculando as raízes, obtemos:
Para determinar qual é de máximo e qual é de mínimo, vamos substituir em e verificar qual é maior e qual é menor.
Portanto em temos um ponto de mínimo em e em temos um ponto de máximo em que .
Assim, vemos que uma janela boa para podermos ver essas informações deve ser um pouco maior que os intervalos desses pontos, então podemos definir uma janela como e :
Tranquilo até aqui?
Passo 3
Agora temos que esboçar o gráfico de ...
Perceba que quando for muito grande, tambem será muito grande (a mesma coisa se for muito grande negativamente, tambem será grande negativamente).
Então tende a se tender a e se tende a , tambem tende a .
Vimos tambem que os pontos e são extremos locais e que é uma raiz de .
Unindo essas informações em um gráfico, podemos esboçar como
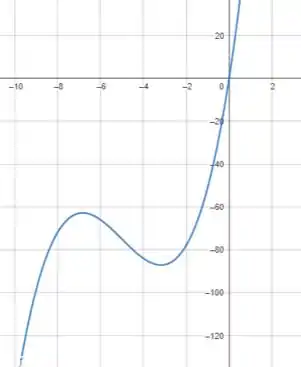
E aí! o que achou? Responde Aí!
Resposta
e