Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 87d
Faça o gráfico das funções e juntamente com seus:
d) dois quocientes.
Passo 1
Antes de começarmos a avaliar os quocientes dessas duas funções, primeiramente vamos construir o gráfico de ambas, ok?
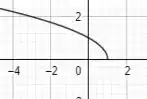
A seção 1.2 do George discute essas duas funções e ainda plota seus gráficos. Sendo assim, o gráfico de é:
E o gráfico de é:
Unindo o gráfico de ambas em um só, teremos:
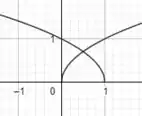
Passo 2
Agora que construímos o gráfico de ambas as funções conseguimos analisar os quocientes das mesmas. Mas por que estamos falando de “quocientes”, no plural? Diferentemente da soma e do produto, a comutatividade NÃO vale para a divisão!
Portanto teremos dois gráficos e não apenas um, como aconteceu com a soma e o produto. Mas po, como que eu faço para dividir essas duas funções aí? Então gente, pelo gráfico conseguimos notar que o domínio dessas duas funções é [0,1) e (0,1]. Dessa forma, a maneira mais interessante e tranquila de esboçar o gráfico dos quocientes dessas funções é pegarmos 3 pontos pertencentes à esse domínio e substituirmos em ambas às funções e, por fim, dividir seus resultados. Relaxa, só parece difícil, mas garanto que não é. Olha só!
Fazendo primeiro para :
Primeiro ponto:
Como o domínio desse quociente não está definido em , então isso significa que o gráfico tende a , mas nunca o toca.
Terceiro ponto:
Fazendo agora para
Como o domínio desse quociente não está definido em , então isso significa que o gráfico tende a , mas nunca o toca.
Segundo ponto:
Terceiro ponto:
Passo 3
Agora que descobrimos 3 pontos importantes e que são comuns às duas funções, se esboçarmos esses pontos no gráfico, teremos:
Para
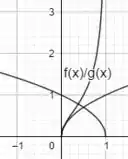
Para
Resposta
Para
Para