Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 80
O exercício a seguir apresenta uma equação de elipse. Coloque a equação no formato padrão e esboce a elipse.
Passo 1
De início já notamos que a equação não está no formato padrão da equação de elipse. O formato padrão é o seguinte:
Assim como discutido na seção 1.2 do George, o gráfico dessa equação para apresenta eixo principal horizontal. Caso contrário, se , o gráfico dessa equação apresenta eixo principal vertical. Em ambos os casos, o eixo principal tem o maior comprimento.
Pessoal, não se assustem com essas duas letras novas ( e )! Quando temos uma equação de elipse nesse formato, significa que o centro da elipse vai ser em , tudo bem? Se liga!
Passo 2
Como o lado direito da equação tem que dar 1, então vamos dividir todos os membros da equação por 4, tranquilão? Além disso, vamos escrever a soma como uma subtração, assim como pede o formato padrão, ok? Fazendo essas duas coisas, teremos a seguinte equação:
Simplificando o que dá para ser simplificado, teremos a seguinte equação:
e
Passo 3
Agora que temos os valores de e e a equação da elipe no formato padrão, conseguimos plotar o gráfico da elipse de boa! Mas vale um adendo: o centro da elipse não vai ser mais em , vai ser em ! Dessa forma, o gráfico vai ficar dessa maneira:
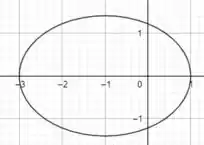
Resposta
