Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.4 - Ex. 7
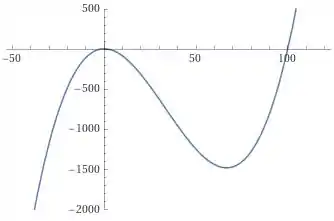
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função
Passo 1
Uma janela retangular são a faixa de valores de e para os quais iremos mostrar o gráfico da nossa função. Quanto maior a janela, maior será o gráfico da nossa função.
Temos a função
Essa é uma função do terceiro grau e, para ela, devemos pegar uma janela gráfica de tal forma que não fique parecendo uma função do segundo grau ou uma reta.
Por ser uma função de terceiro grau, ela possui dois pontos críticos (pontos de máximo ou mínimo) e ela pode ter até três raízes reais distintas (pontos onde a função cruza o eixo ).
Passo 2
Dessa forma, nosso retângulo deverá revelar um ponto de mínimo e também um ponto de máximo, e todas as raízes da nossa função.
Essa escolha é dada por tentativa e erro. Ou seja, escolhe uma janela e caso ela não apresente tudo que a função possui, vai aumentando a sua janela.
Comecei aqui tentando uma janela dada por e .
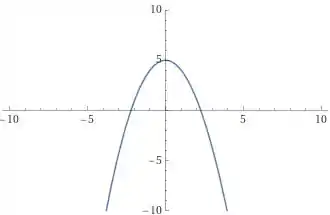
Repare que obtive o gráfico de uma função de segundo grau (um ponto de máximo e duas raízes reais). Ou seja, precisamos aumentar essa janela.
Passo 3
Para ver o que acontece mais abaixo, vou aumentar os valores de negativo da nossa janela, usando portanto e .
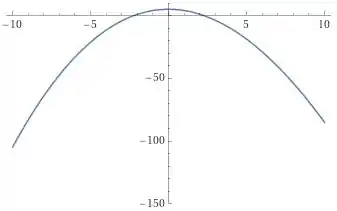
Agora os valores passam no eixo , tanto positivo quanto negativo, por isso, vamos aumentar horizontalmente nossa janela agora.
Vou usar aqui, e .
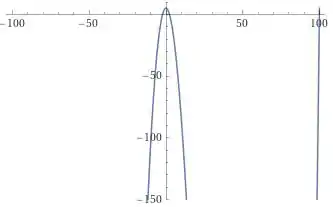
Opa, conseguimos aí, meio que sem querer, encontrar as três raízes da nossa função.
Repara que tem coisa acontecendo ali embaixo, hein...
Passo 4
Para ver o comportamento lá embaixo que a janela anterior não pegou, vou aumentar os valores de negativos.
Usando agora a janela e
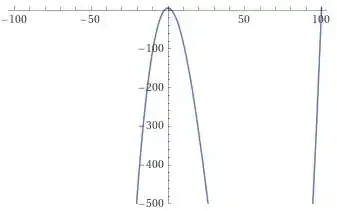
Ainda tem mais coisa para baixo hein... vou aumentar a janela até encontrar aquele ponto de mínimo que está escondido ali.
Usando e
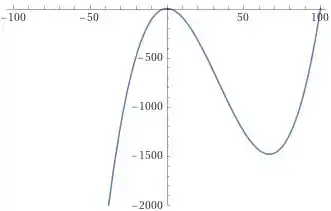
Opaaa, agora sim temos uma função de terceiro grau.
Passo 5
Para fechar, só vamos dar uma ajeitada nisso aí. Repara que eu não preciso ir tão longe no negativo, e que eu posso mostrar um pouco mais os valores depois que e.
Por isso, vou usar a janela: e
