1. O que é uma função um a um?
2. A partir do gráfico, como dizer se uma função é um a um?

a) Uma função um a um (também chamada de injetora) é uma função na qual cada elemento do domínio é associado a no máximo um elemento no contradomínio. Em outras palavras, para cada valor de entrada (do domínio), há apenas um valor correspondente de saída (do contradomínio). Não pode haver dois elementos distintos no domínio que sejam associados ao mesmo elemento no contradomínio.

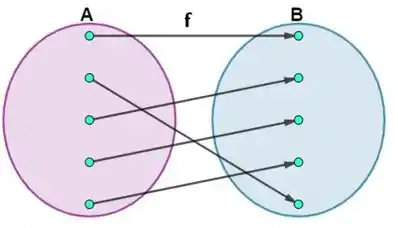
Analisando o diagrama, podemos perceber que essa é uma função injetora. Veja que não existe dois elementos do conjunto A ligados a um mesmo elemento do conjunto B, isso significa que dois elementos distintos do conjunto A sempre possuem imagens diferentes no conjunto B, o que faz com que essa função seja injetora.

b) Para determinar se uma função é um a um a partir do gráfico, você pode usar o teste da linha horizontal, que consiste em traçar linhas horizontais ao longo do eixo vertical (eixo das ordenadas) e ver se elas intersectam a função em no máximo um ponto. Se uma linha horizontal intersectar a função em mais de um ponto, então a função não é um a um. Por outro lado, se cada linha horizontal intersectar a função em no máximo um ponto, então a função é um a um. Em resumo, se não houver duas ordenadas diferentes que correspondam ao mesmo valor de abscissa, a função é um a um.

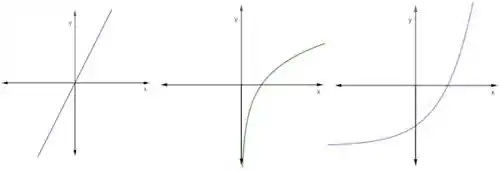
Analisando o gráfico, é possível perceber que qualquer valor de y nos gráficos apresentados é imagem de um único valor.