Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.5 - Ex. 26

Um isótopo do sódio,   N a 24 , tem uma vida média de 15   h o r a s . Uma amostra desse isótopo tem massa de 2 g .

  1. Encontre a quantidade remanescente após 60 horas.
  2. Encontre a quantidade remanescente após t horas.
  3. Estime a quantidade remanescente após 4   d i a s .
  4. Use um gráfico para estimar o tempo necessário para que a massa fique reduzida a 0,01 g .

Passo 1

E aí, pessoal!

Foi fornecido no enunciado que o tempo de meia vida do Sódio é de 15   h o r a s .

A partir de uma amostra de 2 g queremos determinar a quantidade de sódio após 60 h , t horas, 4 dias e a partir desses valores queremos esboçar o gráfico da concentração de sódio em função do tempo e estimar o tempo necessário para que a massa se reduza a 0,01 g .

Parece complicado?

O segredo desse problema é que a cada tempo de meia vida, a concentração de sódio diminui pela metade, ou seja, a cada 15 h .

Já a concentração de sódio é calculada usando essa informação como

y = m 1 2 n

Onde m é a massa e n é o número de ciclos de meia vida

n = t 15

Veja só!

Passo 2

Sendo assim, 60   h o r a s representar 4 tempos de meia vida

n = 60 15 = 4

Portanto podemos calcular a concentração de sódio a partir da equação do passo 1

y = m 1 2 n

y 60 h = 2 1 2 4 = 1 8 g

Tranquilo até aqui?

Passo 3

Para encontrarmos a quantidade que vai sobrar após passar t horas, vemos observar que em t horas temos t / 15 tempos de meia vida, logo a nossa equação será dada por

y = 2 ⋅ 1 2 t 15

Show?

Passo 4

Para estimarmos quanto de massa vai sobrar após 4   dias devemos fazer o seguinte:

4   d i a s = 4 ⋅ 24   h o r a s = 96 h o r a s

Substituindo na equação do passo anterior t = 96 vamos ter:

y = 2 ⋅ 1 2 96 15 ≈ 0,024 g    

Vamos esboçar o gráfico de y partindo de y = 2 e a cada 15 unidades y tem que cair para metade...

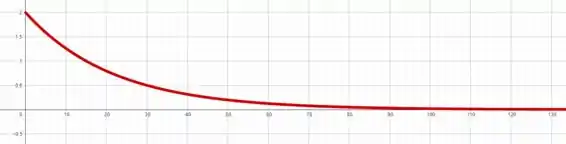
A partir do gráfico podemos estimar que quando y = 0,0 1

t ≈ 114,7   h o r a s

E aí! entendeu tudo? Responde Aí!

Resposta

( a )

1 8 g

b

y = 2 ⋅ 1 2 t 15

( c )

0,024 g

( d )

t ≈ 114,7   h o r a s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

É dado do gráfico de f . Esboce os gráficos das seguintes funções:c) - 2 f x
b) Como estão relacionados o gráfico da função y = 1 +x e o de y = x Use sua resposta e a figura 4 para esboçar o gráfico de y = 1 +x
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção 1.2 e então aplicando as transformações apropriadas. y = x - 1 3
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção 1.2 e então aplicando as transformações apropriadas. y = 4s e n ( 3 x )
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção 1.2 e então aplicando as transformações apropriadas. y = -x 3