Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 10

Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.

Passo 1

E aí, explorador de funções! Pronto para desvendar os mistérios da "janela retangular"? ️‍

Imagine que o gráfico da função é um mapa enorme e cheio de detalhes. A "janela retangular" é como uma lupa poderosa que você usa para explorar esse mapa.

Com a lupa, você pode escolher quais partes do mapa quer ver de perto, focando em detalhes específicos. Da mesma forma, a janela retangular te permite escolher quais partes do gráfico você quer visualizar na tela da sua calculadora ou computador.

Mas como essa lupa mágica funciona?

A máquina que faz o gráfico da função trabalha como um cartógrafo diligente. Ela marca diversos pontos no mapa, conectando-os para formar o gráfico.

Os pontos são marcados em intervalos regulares, como se a máquina estivesse seguindo uma trilha pré-definida. Essa trilha começa em um ponto e termina em um ponto , que você pode escolher para definir a "largura" da sua lupa.

Da mesma forma, você também pode escolher a "altura" da lupa, definindo os pontos e . Dessa forma, você controla quais valores da função serão mostrados na tela.

Por que escolher a janela certa é importante?

Uma janela mal escolhida pode te levar a conclusões erradas sobre o gráfico da função. ⚠️Se você escolher uma janela retangular muito pequena para o gráfico da função, você pode perder detalhes importantes e ter uma visão distorcida do comportamento da função.

Dicas para escolher a janela ideal:

Comece com uma janela ampla para ter uma visão geral da função.
Ajuste a janela para focar em áreas de interesse, como pontos de máximo ou mínimo.
Experimente diferentes janelas para obter diferentes perspectivas do gráfico.
Use o zoom para ampliar áreas específicas do gráfico.
Anote os valores de , , e para referência futura.

Com essas dicas, você estará pronto para explorar o mundo das funções com maestria!

Uma forma de encontrarmos a janela retangular é analisarmos o domínio e a imagem da função. E a partir daí encontrarmos os valores . E é isso que iremos fazer aqui.

Passo 2

Então meu amigo, vamos começar analisando a nossa função:

resulta da expansão da função básica por um fator de . E isso afeta o período da função, e para a gente, que está buscando entender o comportamento do gráfico a parte de um recorte dele, é interessantes estarmos em um intervalo maior que 2 periodos, para melhor visualização e compreesão do gráfico da função.

O período de é , o período de é:

O período nos ajuda a escolhermos o nosso intervalo . Em relação a escolha do intervalo de , poderemos escolher um intervalo um pouco maior que o seu período, tanto para valores positivo e para negativos de , pois assim poderemos ver o comportamento do gráfico tanto no em quanto em .

Como a função trigonométrica é limitada:

Já temos um intervalo superior a escolher, para melhor visualização devemos tomar então como limitantes valores um pouco maiores que .

Passo 3

De inicio, vamos tomar a janela . Como momentado, ambos os intervalos maiores que os valores que encontramos.

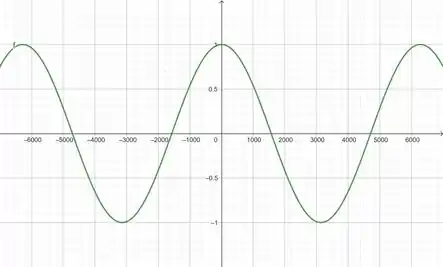
No gráfico podemos ver todas as características da função, seus limitantes superiores e inferiores além da sua perioticidade. Então a janela que escolhemos é satisfatória.

É isso, um forte abraço e até a próxima.