Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 7
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Eaee!!! Belezinha?
Bom... a questão quer que determinemos uma janela retangular apropriada para a seguinte função:
Bom... uma janela apropriada é aquela que dá pra gente obter as principais características de um gráfico, como pontos de máximo e mínimo, bem como os zeros da função.
Assim, a gente pode começar procurando os pontos de máximos e mínimos dessa função e, em seguida, analisamos seus zeros.
A partir daí podemos definir uma janela que englobe todos esses detalhes.
E aí? Bora lá?? 😉
Passo 2
Então... vamos primeiro determinar os zeros da função:
Pra isso fazemos
Portanto é uma das opções...
Continuando os cálculos...
Com isso vemos que , e são os zeros da função, então nossa janela tem que englobar esse intervalo.
Tranquilo até aqui?
Passo 3
Derivando a equação pelo método de derivação polinomial e igualando a zero, podemos encontrar os pontos de máximo e mínimo:
Como pode ser tanto positivo quanto negativo, temos
Calculando os valores de correspondentes, podemos determinar qual desses pontos corresponde ao ponto de máximo e qual corresponde ao ponto de mínimo.
Portanto, é um mínimo local em e é um máximo local em
Dessa forma, a nossa janela precisa incluir esses pontos.
Assim, podemos concluir que uma janela retangular apropriada para a função é por
Show?
Passo 4
Agora vamos condensar as informações que encontramos até aqui para esboçar o gráfico da função.
Vimos que a função possui três zeros... uma em , outra em e a última em .
Além disso vimos que e são os pontos de máximo e mínimo respectivamente e precisam estar na nossa janela.
Além disso, analisando a função
Vemos que aumenta conforme cresce e diminui conforme diminui, logo, tende a se tende a e tambem tende a se tende a .
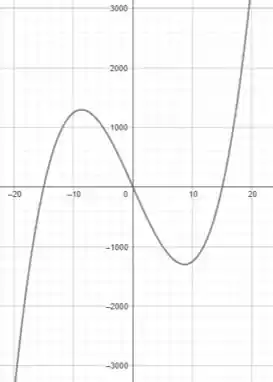
Entendeu direitinho? Responde Aí! ;)
Resposta
por