Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 11
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Olá, meu amigo. Estarei hoje te ajudando a resolver essa atividade.
A atividade nos pede para encontrarmos a janela retangular apropriada da função dada. Mas o que isso quer nos dizer de fato?
Em uma calculadora gráfica, ou até mesmo um computador superpoderoso, a exibição do gráfico é feita por meio de um recorte retangular, não o gráfico por completo. Esse recorte retangular do gráfico é chamado janela de exposição, tela de inspeção ou janela retangular.
A máquina faz o gráfico da função da mesma forma que você o faria. Ela marca pontos da forma para uma certa quantidade de valores igualmente espaçados de entre e . Se um valor não está no domínio de , ou se estiver fora da janela retangular, ela vai para o próximo valor de .
Então para construirmos uma janela retangular apropriada, deveremos assim como as calculadoras gráficas, encontrarmos a variação de de até e os valores de de até , e nossa parte visível do gráfico será o retângulo:
Que pode ser vista abaixo como:
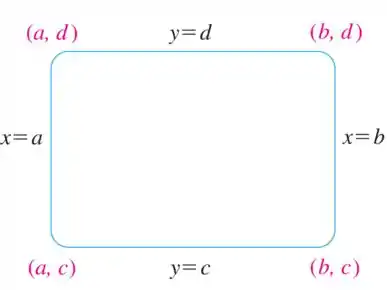
Uma forma de encontrarmos a janela retangular é analisarmos o domínio e a imagem da função. E a partir daí encontrarmos os valores . E é isso que iremos fazer aqui.
Passo 2
Temos então a função:
Vamos dividir essa função em duas, para que possamos entender melhor como encontrar os intervalos.
Iremos chamar de
E
então:
O domínio de , são todos os números reais positivos:
E consequentemente o domínio de também, pois é que nos diz quais valores serão aceitos pela função .
Em relação a imagem da nossa função, vale lembrar que
Isso é, a imagem de é
Pois estamos limitados pela função , e independente do valor de , a função vai ter essa sua limitação.
Não é fácil encontrar a janela retangular apropriado analisando as propriedades da função, mas já que conhecemos o intervalo de , podemos restringir a parte vertical da janela retangular a
maior que a imagem para que possarmos ter uma melhor visualização e tentar com diferentes partes horizontais até encontrarmos uma janela retangular que mostre todos os principais traços do gráfico.
Já que conhecemos o domínio de , devemos iniciar a parte horizontal do Retângulo de Visualização com .
Passo 3
Veja bem, agora iremos procurar de fato um trecho do gráfico que consiga melhor representar o gráfico que queremos. Iremos fazer isso a partir da análise que fizemos da janela retangular.
Primeiro vamos tentar com , para essa tarefa iremos utilizar o GeoGebra, mas fique à vontade para utilizar a sua ferramenta gráfica favorita.
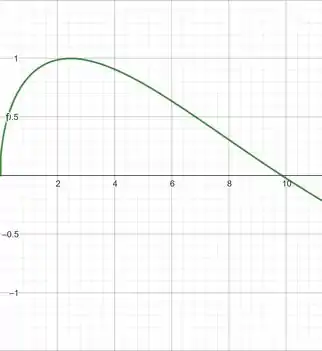
agora vamos tentar com :
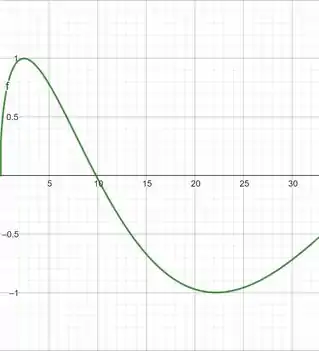
Primeiro vamos tentar com :
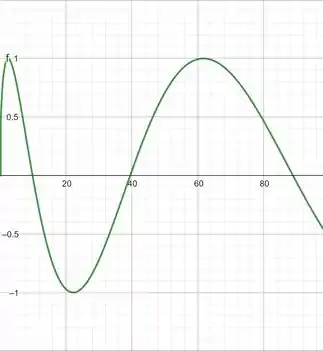
Primeiro vamos tentar com :
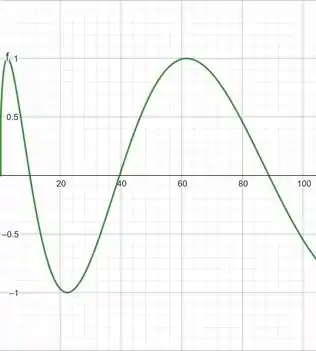
Primeiro vamos tentar com :
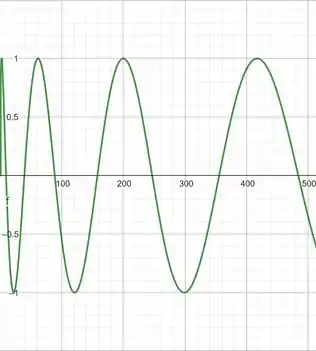
Primeiro vamos tentar com :
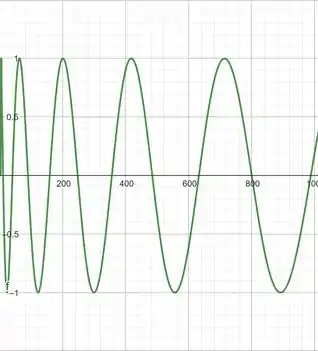
Pela visualização dos gráficos, vemos que a partir de
Já conseguimos ter uma boa noção do comportamento do gráfico. E é isso, um forte abraço meu amigo e até uma próxima.