Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.6 - Ex. 27
Determine o limite QUOTE _x0001_
Passo 1
Nosso objetivo é encontrar um número que representa o limite, desde ele exista, certo? Então temos que se ligar que assim como nos outros cálculos de limites, podemos usar aquelas regras do produto, da soma, do quociente e etc...
Como no limite que devemos calcular temos vários termos em função de QUOTE _x0001_
.
Mas antes, vamos reescrever nosso limite pra facilitar nosso trabalho...
Lembrando que QUOTE _x0001_
, temos
Passo 2
Dividindo todo mundo por QUOTE _x0001_
,
QUOTE _x0001_
Passo 3
Se fuçarmos a memória, lembraremos que QUOTE _x0001_
. Então, nossas contas ficam
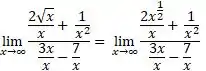
Passo 4
Tirando mais uma vez do fundo do baú das lembranças, QUOTE _x0001_
. Substituindo em nossas contas,
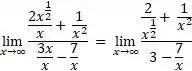
Passo 5
Usando a regra do quociente: “O limite do quociente é o quociente dos limites”, temos:
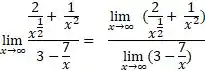
Passo 6
Usando que o limite da soma é a soma dos limites e, da mesma forma pra a subtração,
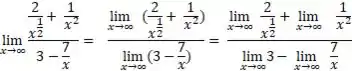
Passo 7
Como 3 não depende de QUOTE _x0001_
,
E, lembrando que QUOTE _x0001_
, sacou por que?
Vou tentar ilustrar rapidinho:
Imagine que você tem R$100,00 para dividir para nós dxs, beleza ? Então, a quantidade que vamos receber seria R$50,00 Mas e se agora você tiver que dividir para cem pessoas, o valor vai ser bem menor, não é ? Mas e se for para mil pessoas? Menor ainda, concorda comigo, migxs? Então, o valor recebido por cada um de nós é cada vez menor à medida que aumentamos a quantidade de pessoas que temos que dividir o money, ou seja, estamos ficando com quase nada, né?!! O valor a receber por nós tende a zero.
Tá, se olharmos para esse R$100,00 como nosso 2 e fazermos QUOTE _x0001_
tender a infinito é como se estivessemos dividindo o 2 por valores cada vez maiores, consequentemente
QUOTE _x0001_
Da mesma forma,
Substituindo essas coisas todas em nossas contas,
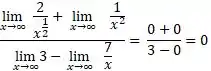
Então,
Resposta
