Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.2 - Ex. 19
A tabela dá as alturas dos vencedores do salto com vara nas Olimpíadas durante o século .
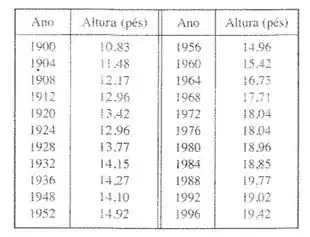
- Faça um mapa de dispersão e decida se um modelo linear é apropriado
- Encontre e faça um gráfico da reta de regressão.
- Use o modelo linear para predizer qual a altura do vencedor nas Olimpíadas de e compare com a altura do vencedor de .
- É razoável usar o modelo para predizer a altura do vencedor para as Olimpíadas de
Passo 1
Opa, bora lá! A questão toda é baseada em substituir os dados presentes na tabela em um software matemático ou no Excel mesmo para obtermos os gráficos desejados pela questão. Dessa forma, selecionando os anos como eixo e a altura como eixo , teremos:
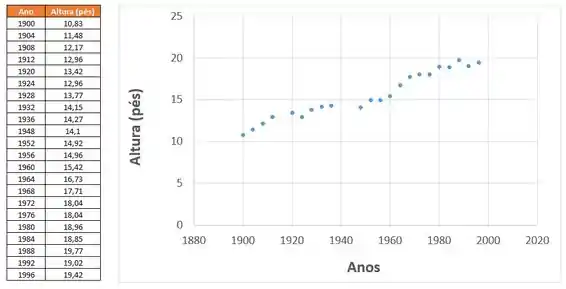
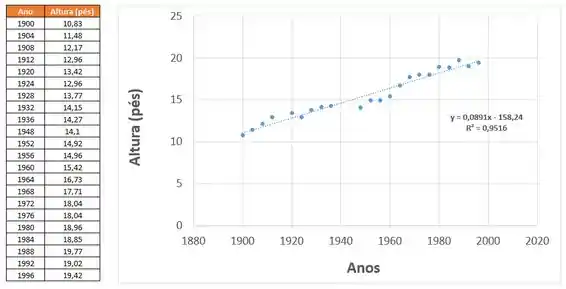
A partir desse gráfico podemos traçar uma linha de regressão que mostra a tendência que nossas amostras estão seguindo e como os dados estão bem próximos uns dos outros podemos dizer que um modelo linear se mostra apropriado para esse modelo. Obteremos, assim, o seguinte:
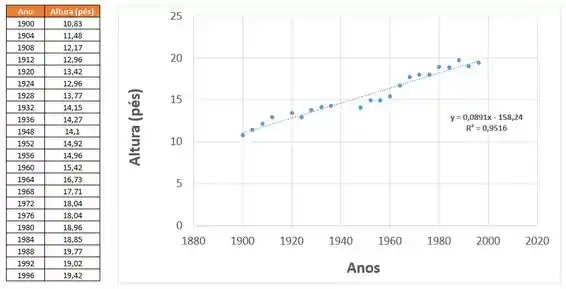
Aplicando o modelo de regressão linear obtemos a seguinte equação de aproximação
Onde:
- está em anos
- está em pés
E pela fórmula, obtemos:
- Quando tivermos um valor de , vamos obter .
- Por outro lado, inserindo , encontramos
Conclusão:
Para efeitos comparativos vemos que o vencedor das olímpiadas dos anos iria bater o recorde do vencedor de , que foi de , em apenas , estabelecendo neste ano o novo recorde de
Passo 2
Utilizando da fórmula:
Podemos prever que no ano de , teremos um recorde de . Note que, apesar de o , que expressa pra gente o quão bem essa equação ajustou nossos dados (quanto mais próximo de melhor), ser alto, para o ano de o nosso modelo não é tão razoável de ser aplicado, haja vista que teríamos um aumento de na altura do campeão dos anos , o que é pouco improvável.
Resposta
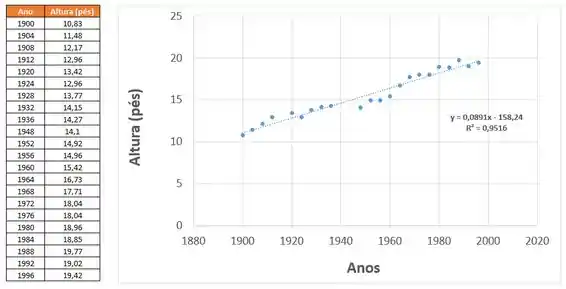
- Para efeitos comparativos vemos que o vencedor das olímpiadas dos anos iria bater o recorde do vencedor de , que foi de , em apenas , estabelecendo neste ano o novo recorde de
- Podemos prever que no ano de , teremos um recorde de , o que representa um aumento de na altura do campeão dos anos , algo pouco improvável. O modelo não é bom para esse ano.