Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 80
Determine os pontos aos quais a curva tem retas tangentes horizontal e vertical. Faça um esboço gráfico com essas retas tangentes.
Passo 1
Primeiro, em questões que envolvem retas tangentes, sempre temos aquelas equaçõeszinhas que não podem se perderem na nossa mão!! Aí vão elas:
Logo, para o nosso caso, temos que:
Portanto:
Passo 2
Agora vamos resumir a nossa equação para então encontrarmos os pontos em que nossa retas são tangentes.
Para a nossa equação, temos esse esboço:
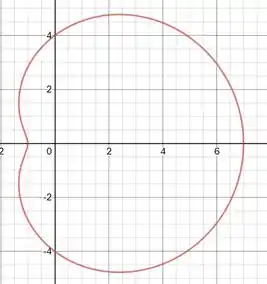
Sim, a nossa equação é quase um cardioide!! Para isso, temos que nossos pontos são de:
Passo 3
Sabendo disso, temos que as nossas retas se encontram em x=-1 e x=
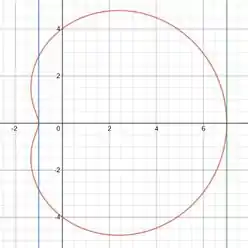
Resposta
Retas:
X=-1
X=7
Exercícios de Livros Relacionados
Coloque cada equação na forma padrão e encontre as assíntotas da hipérbole. Em seguida, esboce a hipérbole. Inclua as assíntotas e focos no seu esboço. 9 x 2 - 16 y 2 = 144
A região delimitada à esquerda pelo eixo y, à direita pela hipérbole x2 - y2 = 1 e acima e abaixo pelas retas y = ±3, é girada em torno do eixo y para gerar um sólido. Encontre o volume do sólido.
É fornecida a equação para a hiperbole. Coloque cada equação na forma padrão e encontre as assíntotas da hipérbole. Em seguida, esboce a hipérbole. Inclua as assíntotas e focos no seu esboço. y 2 - x
Mostre que as tangentes à curva y2 = 4px a partir de qualquer ponto na reta x = –p são perpendiculares.
Encontre equações para as tangentes do círculo (x - 2)2 + (y - 1)2 = 5 nos pontos em que o círculo cruza os eixos coordenados.