Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.7 - Ex. 31

Determine o valor de ∫ ∫ S x 2 y 2 z 2   d S   correto até a quarta casa decimal, onde S é a parte do paraboloide z = 3 - 2 x 2 - y 2 que está acima do plano x y .

Passo 1

Fala, pessoal! Tudo bem?

A questão pede o valor de

∫ ∫ S x 2 y 2 z 2   d S

Com precisão de até 4 casas decimais. No livro temos o símbolo ao lado dessa questão, o que significa que vamos precisar usar um software ou calculadora para obter o valor dessa integral. Podemos usar o software WolframAlpha. E para isso falta determinarmos nossos limites de integração e calcular nosso termo:

d S = d z d x 2 + d z d y 2 + 1   d x d y

Bora lá, então!

Passo 2

Com os dados que nos foram fornecidos, podemos calcular o jacobiano dessa superfície da seguinte forma:

d S = d z d x 2 + d z d y 2 + 1   d x d y

O enunciado traz que S é a superfície:

z = 3 - 2 x 2 - y 2

Calculando suas derivadas parciais. Derivando em x , tratando y como constante:

d z d x = d 3 - 2 x 2 - y 2 d x = - 4 x

Derivando em y , tratando x como constante:

d z d y = d 3 - 2 x 2 - y 2 d y = - 2 y

Então, substituindo na equação de d S :

d z d x 2 + d z d y 2 + 1   d x d y = - 4 x 2 + - 2 y 2 + 1   d x d y

Elevando os termos ao quadrado:

d S = 16 x 2 + 4 y 2 + 1

Passo 3

Note que ainda não temos os limites de integração da nossa integral dupla, já que o enunciado não nos trouxe essa informação. Vamos tirar essa informação da restrição:

z = 3 - 2 x 2 - y 2 que está acima do plano x y

Ou seja:

z = 3 - 2 x 2 - y 2 onde z > 0

Para estar acima do plano x y e isso nos dá:

3 - 2 x 2 - y 2 > 0

Isolando y 2 :

y 2 < 3 - 2 x 2

Tirando a raiz quadrada, vemos que y pode assumir o valor negativo dessa inequação, já que y está elevado ao quadrado:

- 3 - 2 x 2 ≤ y ≤ 3 - 2 x 2

E se zerarmos y , obtemos os valores no eixo x , nossa inequação fica:

3 - 2 x 2 - 0 > 0

Isolando x :

- 3 2 ≤ x ≤ 3 2

Pronto, achamos os limites de integração!

Passo 4

Então a integral de superfície será:

∫ - 3 2 3 2 ∫ - 3 - 2 x 2 3 - 2 x 2 x 2 y 2 3 - 2 x 2 - y 2 2 16 x 2 + 4 y 2 + 1   d y   d x  

Utilizando o WolframAlpha temos a seguinte resposta:

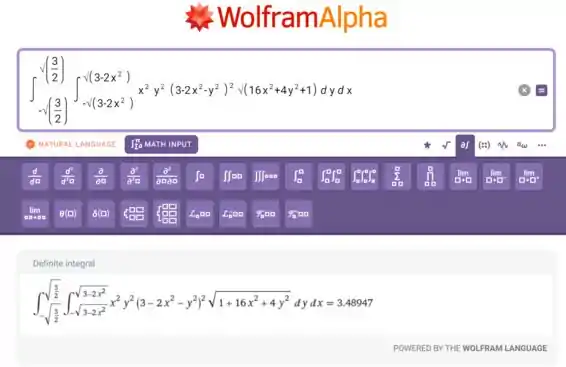
Com 4 casas decimais temos:

∫ - 3 2 3 2 ∫ - 3 - 2 x 2 3 - 2 x 2 x 2 y 2 3 - 2 x 2 - y 2 2 16 x 2 + 4 y 2 + 1   d y   d x  

= 3 , 4895

Resposta

3 , 4895

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Avalie a integral de superfície ∬ S F → ⋅ d S → para o campo vetorial dado F → e a superfície orientada S . Em outras palavras, localize o fluxo de F através deS . Para superfícies fechadas, use a ori
Avalie a integral de superfície ∬ S F → ⋅ d S → para o campo vetorial dado F → e a superfície orientada S . Em outras palavras, localize o fluxo de F através deS . Para superfícies fechadas, use a ori
Avalie a integral de superfície ∬ S F → ⋅ d S → para o campo vetorial dado F → e a superfície orientada S . Em outras palavras, localize o fluxo de F através deS . Para superfícies fechadas, use a ori
Avalie a integral de superfície ∬ S F → ⋅ d S → para o campo vetorial dado F → e a superfície orientada S . Em outras palavras, localize o fluxo de F através deS . Para superfícies fechadas, use a ori
Calcule a integral de superfície ∫ ∫ S F → ⋅ d S → para o campo vetorial F → e superfície orientada S . F → x , y , z = x z i ^ + x j ^ + y k ^ , S é o hemisfério x 2 + y 2 + z 2 = 25 , y ≥ 0 , orient