Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.7 - Ex. 25

Avalie a integral de superfície ∬ S F → ⋅ d S → para o campo vetorial dado F → e a superfície orientada S . Em outras palavras, localize o fluxo de F através de   S . Para superfícies fechadas, use a orientação (para o exterior) positiva.

F → x , y , z = x i ^ - z j ^ + y k ^

S é a parte da esfera   x 2 + y 2 + z 2 = 4   no primeiro octante, com orientação para a origem.

Passo 1

Faaaala minha galerinha, beleza!? Vamos nessa!

Nessa questão precisamos encontrar o fluxo de F através da superfície S .

F → x , y , z = x i ^ - z j ^ + y k ^

Onde S é:

parte da esfera   x 2 + y 2 + z 2 = 4   no primeiro octante, com orientação para a origem.

Primeiro vamos pensar na integral para esse caso. Vamos ter que:

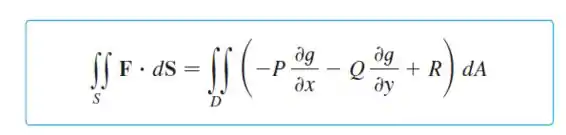
Onde, P   Q   e   R são os termos do campo F → :

F → x , y , z = P i ^ + Q j ^ + R k ^

Já o termo g ( x , y ) que aparece com suas derivadas em relação a x e y é:

g x , y = z =   4 - x 2 - y 2

Importante, essa integral considera um vetor n apontando para fora da superfície. Como o enunciado pede o vetor apontando para a origem, basta multiplicarmos a integral por - 1 .

A figura abaixo, vai ajudar a entender essa situação:

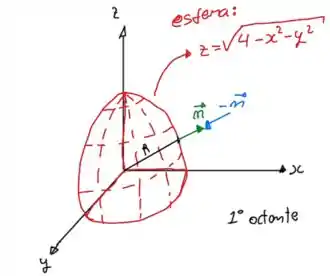
Temos um pedaço da esfera x 2 + y 2 + z 2 = 4 no primeiro octante.

Olhando a região de integração. No plano x y é um quarto de círculo de raio 2   então, em coordenadas polares temos:

x = r c o s θ y = r s e n θ d A = r d r d θ 0 ≤ r ≤ 2 0 ≤ θ ≤ π / 2

Agora é só substituir na integral! E não se esqueça de passar para coordenadas polares, isso vai facilitar.

Bora lá!

Passo 2

Vamos começar organizando os termos para substituir na integral:

∬ S F ∙ d S = - ∬ D ( - P ∂ g ∂ x - Q ∂ g ∂ y + R ) d A

Lembre-se que multiplicamos a integral por - 1 , para fazer a correção do sentido do vetor normal! Que deve ser para a origem!

A função g x , y = z é:

g x , y = 4 - x 2 - y 2

Logo, as derivadas em relação a x e y são:

∂ g ∂ x = - x 4 - x 2 - y 2

∂ g ∂ y = - y 4 - x 2 - y 2

Fazendo a comparação:

F → x , y , z = P i ^ + Q j ^ + R k ^

F → x , y , z = x i ^ - z j ^ + y k ^

Temos que:

P = x

Q = - z

R = y

Substituindo na integral, ficamos com:

∬ S F ∙ d S = - ∬ D ( - x - x 4 - x 2 - y 2 + z - y 4 - x 2 - y 2 + y ) d A

Repara que temos z na integral, e sabemos que z é:

z =   4 - x 2 - y 2

Substituindo, vamos ter:

∬ S F ∙ d S = - ∬ D ( - x - x 4 - x 2 - y 2 + 4 - x 2 - y 2 - y 4 - x 2 - y 2 + y ) d A

Simplificando temos:

∬ S F ∙ d S = - ∬ D x 2 4 - x 2 - y 2 d A

Passo 3

Agora vamos entrar com as coordenadas polares, assim vai facilitar a resolução da integral.

São elas:

x = r c o s θ y = r s e n θ d A = r d r d θ 0 ≤ r ≤ 2 0 ≤ θ ≤ π / 2

Substituindo na integral, temos:

∬ S F ∙ d S = - ∬ D ( r cos ⁡ θ ) 2 4 - ( r cos ⁡ θ ) 2 - ( r   s e n   θ ) 2 d A

∬ S F ∙ d S = - ∬ D r 2 c o s 2   θ 4 - r 2 d A

Usamos a relação trigonométrica abaixo para simplificar a integral acima. Desse jeito:

cos 2 ⁡ θ + s e n 2 θ = 1

Substituindo os intervalos de integração e d A , temos:

- ∫ 0 π / 2 ∫ 0 2 r 3 c o s 2   θ 4 - r 2 d r d θ

Repare em uma coisa, as variáveis r e θ são independentes, certo?

Isso permite a gente fazer as duas integrais simultaneamente. Desse jeito:

- ∫ 0 π / 2 c o s 2   θ   d θ ∙ ∫ 0 2 r 3 4 - r 2 d r

Passo 4

Agora, vamos lembrar de outra relação trigonométrica. A seguinte:

c o s 2   θ = 1 + cos ⁡ 2 θ 2

Substituindo, temos:

- ∫ 0 π / 2 1 2 + 1 2 cos ⁡ 2 θ   d θ ∙ ∫ 0 2 r 3 4 - r 2 d r    

Para a integral de cos ⁡ 2 θ , vamos fazer uma substituição:

v = 2 θ

d v 2 = d θ

Para integrar em r , vamos usar a substituição:

u = 4 - r 2

Assim:

d u = - 2 r d r ∴ r d r = - 1 2 d u

r 2 = 4 - u

E os limites? Quando r = 0 temos que u = 4 e quando r = 2 temos que u = 4 - 4 = 0 .

Então substituindo temos:

- ∫ 0 π / 2 1 2   d θ + ∫ 0 π / 2 1 2 cos ⁡ v d v 2   ∙   ∫ 4 0 - 1 2 4 - u u - 1 2   d u

Passo 5

Agora sim podemos resolver as integrais.

Integrando e voltando para a variável θ , temos:

- θ 2 + 1 4 s e n 2 θ 0 π / 2 ∙ - 1 2   8 u - 2 3 u 3 2 4 0

Agora vamos aplicar os limites. Aplicando, temos:

- π 4 + 1 4 s e n 4 π - 0 2 + 1 4 s e n 0 - 1 2 0 - 0 - 8 4 - 2 3 4 3 2

Resolvendo, ficamos com:

- π 4 + 0 - 0 + 0 ∙ - 1 2 0 - 0 - 16 - 2 3 8

- π 4 - 1 2 - 16 + 16 3

E resolver essas últimas multiplicações, vamos ter que a integral de superfície vale:

∬ S F → ⋅ d S → = - 4 3 π  

Resposta

∬ S F → ⋅ d S → = - 4 3 π  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ SF ⋅ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p