Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 32

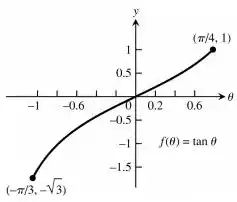
Determine os valores mínimo e máximo absolutos de cada função nos intervalos dados. Em seguida, esboce o gráfico da função. Identifique os pontos no gráfico em que os extremos absolutos ocorrem e inclua suas coordenadas.

Passo 1

Para determinar os valores máximo e mínimo absolutos, podemos fazer a derivada da função dada e igualar este resultado a zero (encontrar ponto(s) crítico(s)). Fazendo esse procedimento, temos que:

A primeira derivada da função fornecida não possui solução, ou seja, não possui nenhum ponto crítico.

Assim, caso existam extremos absolutos, eles serão determinados através do esboço do gráfico da função.

Passo 2

Fazendo o esboço do gráfico da função é possível tirar algumas conclusões sobre a função e, também, verificar se existem extremos absolutos e onde eles existem. Nesse caso, o intervalo é fechado, portanto podemos verificar os pontos extremos desse intervalo.

Passo 3

Logo, para saber as coordenadas de cada ponto em que existe um extremo absoluto temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

51-60 Dê um gráfico de polinômio e identifique as coordenadas dos cortes com os eixos, dos pontos estacionários e dos pontos de inflexão. Confira as respostas com um recurso gráfico.57- p x = x 4 - 2

Esboce o gráfico de y=x–a m x–b n para os valores indicados de m e n , supondo ab (seis gráficos no total). (c) m=3 ,n= 3

Esboce o gráfico de y=x–a m x–b n para os valores indicados de m e n , supondo ab (seis gráficos no total). (b) m=2 ,n= 2 ,3

Esboce o gráfico de y=x–a m x–b n para os valores indicados de m e n , supondo ab (seis gráficos no total). (a) m=1 ,n=1 ,2 ,3

Mostre que o valor mínimo absoluto de f x = x 2 + x 2 8 - x 2 , x8 ocorre em x=10 usando um CAS para encontrar f ' ( x ) e para resolver f ' ( x )=0 .