Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.2 - Ex. 57

51-60 Dê um gráfico de polinômio e identifique as coordenadas dos cortes com os eixos, dos pontos estacionários e dos pontos de inflexão. Confira as respostas com um recurso gráfico.

57- p x = x 4 - 2 x 3 + 2 x - 1

Passo 1

Galera, vamos começar derivando a função:

p ´ x = 4 x 3 - 6 x 2 + 2

Agora, vamos derivar novamente:

p ´ ´ x = 12 x 2 - 12 x

Passo 2

Igualando a primeira derivada a zero, temos:

p ´ x = 0

4 x 3 - 6 x 2 + 2 = 0

x 1 = 1  

Agora, podemos usar Briot Ruffini para acharmos as outras raízes:

4 x 2 - 2 x - 2 x - 1 = 0

4 x 2 - 2 x - 2 = 0

x 2 = 1   e   x 3 = - 1 2

Para x = 1 :

p 1 = 1 4 - 2 × 1 3 + 2 × 1 - 1 = 0

Para x = - 1 2 :

p 3 = 1 2 4 - 2 × 1 2 3 + 2 × 1 2 - 1 = - 27 16

( 1,0 ) e ( - 1 2 ,   - 27 16 ) são nossos pontos estacionários.

O próximo passo é saber se f ´ ´ x 0 > 0 , f ´ ´ x 0 < 0 ou f ´ ´ x 0 = 0 . Isso que vai determinar qual tipo de extremos relativo nós encontramos.

Passo 3

Para x = 1 :

p ´ ´ 1 = 12 × 1 2 - 12 × 1 = 0

Como p ´ ´ x 0 = 0 temos que usar o teste da primeira derivada. Para isso, temos que fazer o estudo de sinal de p ´ x .   Vamos testar dois pontos, um direita do 1 e o outro a esquerda e ver como essa função se comporta.

Para x = 0 :

p ´ 0 = 2

Para x = 2 :

p ´ 2 = 3

Como a função é > 0 a direita e a esquerda do 1, o ponto ( 1,0 ) não é nem máximo nem mínimo.

Para x = 1 2 :

p ´ ´ - 1 2 = 12 × - 1 2 4 - 12 × - 1 2 = 27 4

Isso quer dizer que o ponto   ( - 1 2 , - 27 16 ) é o nosso mínimo.

Vamos ver se temos algum ponto de inflexão... Para isso nós temos que fazer um estudo de sinais com a função p ´ ´ ( x ) . Então vamos lá!

p ´ ´ x = 12 x 2 - 12 x

p ´ ´ x = 0

12 x 2 - 12 x = 0

12 x ( x - 1 ) = 0

x = 0   e   x = 1

Agora, vamos ver como a função se comporta antes e depois do 0 . Para isso vamos testar um valor de x < 0 e outro valor de x > 0 . Ok ???

Para x = - 1 :

p ´ ´ - 1 = 24

Para x = 0,5 :

p ´ ´ 0,5 = - 3

Como p ´ ´ ( x ) tem sinais diferentes antes e depois do 0 , para x = 0 , temos um ponto de inflexão.

Para x = 0

p 0 = - 1  

O ponto ( 0 ,   - 1 )   é um ponto de inflexão.

Bom... Também temos quer ver como a função se comporta antes e depois do 1 . Para isso vamos testar um valor de x < 1 e outro valor de x > 1 . Ok ???

Para x = 0,5 :

p ´ ´ 0,5 = - 3

Para x = 2 :

p ´ ´ 2 = 24

Como p ´ ´ ( x ) tem sinais diferentes antes e depois do 1 , para x = 1 , temos um ponto de inflexão.

Para x = 1

p 1 = 0  

O ponto ( 1,0 )   é um ponto de inflexão.

Passo 4

Por último, temos que ver os cortes com os eixos.

- Eixo x :

x 4 - 2 x 3 + 2 x - 1 = 0

x 1 = 1  

Agora, podemos usar Briot Ruffini para acharmos as outras raízes:

( x 3 - x 2 - x + 1 ) x - 1 = 0

x 3 - x 2 - x + 1 = 0

x 2 = - 1

Como temos um polinômio de grau 4, esperamos encontrar 4 raízes, dessa forma, vamos usar o Briot Ruffini de novo:

( x 2 - 2 x + 1 ) x + 1 x - 1 = 0

x 2 - 2 x + 1 = 0

x 3   e   x 2 = 1

Caraaaa, isso quer dizer que temos raízes múltiplas !!!!

Os cortes com eixo x são nos pontos:

- 1,0   e   1,0

- Eixo y :

p 0 = - 1

Os cortes com eixo y são nos pontos:

( 0 , - 1 )

Assim, nós temos o seguinte gráfico:

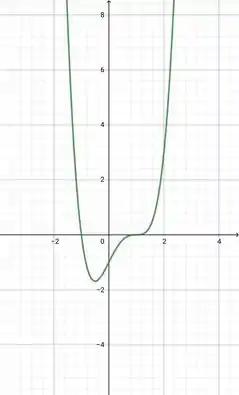
Resposta

( 1,0 ) (nenhum dos dois) e ( - 1 2 ,   - 27 16 ) (mínimo) são nossos pontos estacionários.

0 , - 1   e   ( 1,0 ) são pontos de inflexão.

Cortes nos eixos: - 1,0 , 1,0   e   ( 0 , - 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os valores máximo e mínimo absolutos, se houver, nos intervalos dados e indique onde esses valores ocorrem. f x = 4 x 3 - 3 x 4 ,- ∞ ,+ ∞
Encontre os valores máximo e mínimo absolutos, se houver, nos intervalos dados e indique onde esses valores ocorrem. f x = x 3 - 9 x + 1 ,- ∞ ,+ ∞
Encontre os valores máximo e mínimo absolutos, se houver, nos intervalos dados e indique onde esses valores ocorrem. f x = 2 x 3 - 6 x + 2 ,- ∞ ,+ ∞
Encontre os valores máximo e mínimo absolutos, se houver, nos intervalos dados e indique onde esses valores ocorrem. f x = x - 2 x + 1 ,( - 1,5 ]
Encontre os valores máximo e mínimo absolutos, se houver, nos intervalos dados e indique onde esses valores ocorrem. f x = x 2 + 1 x + 1 ,- 5 , - 1