Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.4 - Ex. 51
Mostre que o valor mínimo absoluto de
ocorre em usando um CAS para encontrar e para resolver .
Passo 1
Cara, é só a gente seguir o passo a passo que a questão descreve para gente. Vamos usar o Wolfram Mathematica para fazer essas continhas.
Primeiro, precisamos achar a derivada dessa função. Fica assim:
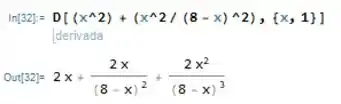
Passo 2
Agora precisamos descobrir onde essa derivada zera. Então precisamos resolver, no intervalo , a equação:
As continhas ficam assim:
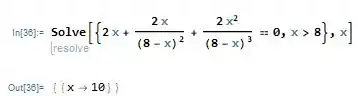
Vemos que a solução para essa equação é . Logo, esse é um ponto crítico da nossa função. E como o enunciado diz, ele é o mínimo da função no intervalo dado.
Resposta
Prova nos passos
Exercícios de Livros Relacionados
Mostre que f x = sec x + c o s s e cx tem um valor mínimo, mas nenhum valor máximo no intervalo 0 , π 2 . Encontre o valor mínimo da parte (a).
Um trapézio é inscrito em um semicírculo com raio 2 , de forma que um lado está sobre o diâmetro (Figura Ex-47). Encontre a maior área possível para o trapézio. [Sugestão: Expresse os lados do trapézi
Um canal de drenagem deve ser feito de tal forma que a secção transversal é um trapézio com os lados igualmente inclinados (Figura Ex-48). Se os lados e a base tiverem um comprimento de 5m , como esco
Encontre os valores máximo e mínimo absolutos de f x = 4 x - 2,s ex1 x - 2 x - 3 , s ex ≥ 1 em 1 2 7 2 .
44. Uma firma determina que x unidades de seu produto podem ser vendidas diariamente a p dólares a unidade, onde: x = 1000 - p O custo de produção de x unidades diárias é: C x = 3000 + 20 x a) Encontr