Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.2 - Ex. 62a
Esboce o gráfico de para os valores indicados de e , supondo (seis gráficos no total).
(a)
Passo 1
Cara, a ideia aqui é usar aquelas implicações geométricas da multiplicidade das raízes dos polinômios para esboçar essas curvas.
Uma raiz de um polinômio vai ter multiplicidade se ele for divisível por e não por , ou seja, se a gente consegue fatorar ele e um dos termos for .
A gente vê que nossas curvas já estam fatoradas. Só precisamos interpretar a multiplicidade dessas raízes e esboçar o gráfico com essas informações.
Vamos lá!
Passo 2
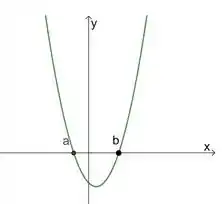
O primeiro caso é quando a gente tem:
Nesse caso, as duas raízes, e , desse polinômio tem multiplicidade , ou seja, são raízes simples.
Quando isso acontece, só podemos afirmar que o gráfico não é tangente ao eixo nesses pontos, mas cruza o eixo neles.
Colocando essas características num gráfico, a gente fica com algo assim:
Passo 3
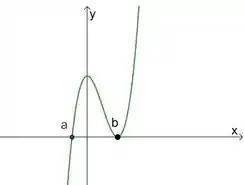
No segundo caso temos:
Nesse caso, a raíz tem multiplicidade . Logo, nesse ponto o nosso gráfico não é tangente ao eixo , mas cruza esse eixo.
Já a raiz tem multiplicidade , ou seja, uma multiplicidade par. Isso diz para gente que o gráfico vai ser tangente ao nesse ponto, mas não vai cruzar o eixo e esse ponto não será um ponto de inflexão.
Colocando essas características num gráfico, a gente fica com algo assim:
Passo 4
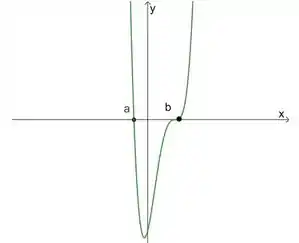
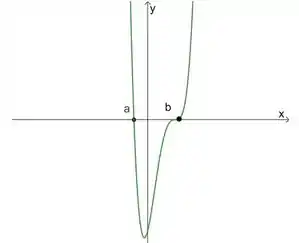
No terceiro caso temos:
Nesse caso, a raíz tem multiplicidade . Logo, nesse ponto o nosso gráfico não é tangente ao eixo , mas cruza esse eixo.
Já a raiz tem multiplicidade , ou seja, uma multiplicidade ímpar e maior que . Isso diz para gente que o gráfico vai ser tangente ao nesse ponto, vai cruzar o eixo e esse ponto será um ponto de inflexão.
Colocando essas características num gráfico, a gente fica com algo assim:
Resposta
Caso 1: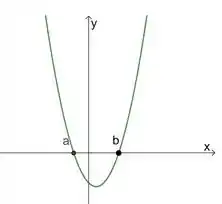 
Caso 2: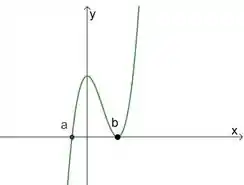 
Caso 3: 