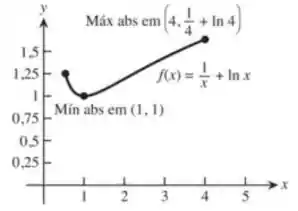
Determine os valores mínimo e máximo absolutos de cada função nos intervalos dados. Em seguida, esboce o gráfico da função. Identifique os pontos no gráfico em que os extremos absolutos ocorrem e inclua suas coordenadas.
![]()
Passo 1
Para determinar os valores máximo e mínimo absolutos, podemos fazer a derivada da função dada e igualar este resultado a zero (encontrar ponto(s) crítico(s)). Fazendo esse procedimento, temos que:
A primeira derivada da função fornecida, depois que igualada a zero, tem como solução. No entanto, este ponto não é um ponto crítico, pelo fato de não estar contido no intervalo do domínio da função.
Assim, caso existam extremos absolutos, eles serão determinados através do esboço do gráfico da função.
Passo 2
Fazendo o esboço do gráfico da função é possível tirar algumas conclusões sobre a função e, também, verificar se existem extremos absolutos e onde eles existem. Nesse caso, o intervalo é fechado, portanto podemos verificar os pontos extremos desse intervalo.
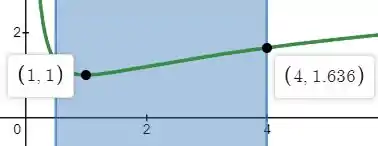

Passo 3
Logo, para saber as coordenadas de cada ponto temos:
Resposta