Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 61
Encontre os valores de máximo e mínimo absoluto de no intervalo dado
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui a questão quer os pontos críticos da função dentro do intervalo .
Números críticos são os pontos no domínio em que uma das seguintes opções é verdadeira: (1) A derivada é 0. (2) O derivado não existe/não está definido.
Iremos avaliar o valor de em cada um dos pontos críticos e também nos pontos extremos. Entre estes, o valor máximo de é o máximo absoluto. E, o valor mínimo de é o mínimo absoluto. Note que haverá apenas um máximo absoluto e um mínimo absoluto. Além disso, observe que tudo isso é verdade apenas quando os intervalos são fechados.
Passo 2
Primeiramente, necessitamos calcular a derivada de para encontrar os números críticos. Os pontos críticos de são os valores de nos quais não existe, ou, se existir, é igual a zero.
Então utilizando a regra da cadeia para derivar:
Igualando a zero
No numerador
Se o denominador for igual a zero, teremos que não estará definido, então também teremos um número crítico, logo, igualando o denominador a zero, ficamos com
Pela fórmula de Baskara
Como essa equação não apresenta uma raiz real, então, no domínio dos números reais, o denominador de nunca será zero.
Passo 3
Para encontrar os valores máximos/mínimos absolutos em um intervalo fechado, avalie os valores funcionais nos números críticos, bem como nos pontos finais. Dentre esses valores, o máximo/mínimo corresponderá ao máximo/mínimo absoluto respectivamente.
Aplicando o método do intervalo fechado, necessitamos calcular . Então
Com isso podemos ver que é um ponto de máximo absoluto e é um ponto de mínimo absoluto.
Visualizando o gráfico da função abaixo que criamos com o GeoGebra, podemos ver que estamos certos:
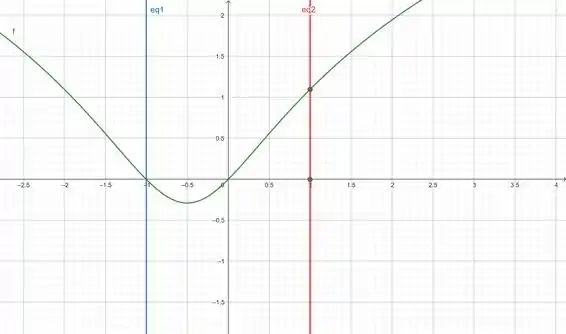
Resposta
é um ponto de máximo absoluto e é um ponto de mínimo absoluto.