Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.2 - Ex. 24
Determine o vetor unitário com mesma direção e sentido que o vetor dado.
Passo 1
Fala povo bonito, tudo certo? Essa questão é bem direto ao ponto. Todo vetor se torna unitário se a gente dividir ele por seu módulo! Perceba ainda que dividir pelo módulo (uma constante positiva) não altera sentido nem direção! Logo quem a qustão pede é esse carinha:
Do nosso enunciado, temos:
Portanto seu módulo será:
O vetor unitário será então:
Passo 2
Aqui nesse passo vamos só checar nossa resposta, tranquilo? Só pra enriquecer mesmo porque respondida a questão já está. O módulo do vetor unitário tem que ser , mas será que é mesmo? Vamos ver:
E olha só os dois vetores num gráfico como ficam:
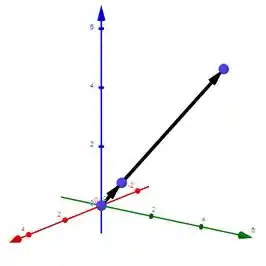
Lindo, não?
Resposta
Exercícios de Livros Relacionados
Observe a Proposição 9-7. Apenas como exercício, pois esta nomenclatura é habitualmente usada, relacione as palavras comutativa e distribuitiva a um ou mais itens do enunciado. Explique a ausência de
Prove que, se a matriz M é ortogonal, então det M = 1 ou det M = - 1 . Vale a recíproca?
Sabendo que u → + v → + w → = 0 → , u → = 3 / 2 , v → = 1 / 2 e w → = 2 , calcule u → ⋅ v → + v → ⋅ w → + w → ⋅ u → .
Sendo u → e v → unitários, w → = 4 , u → ⋅ w → = - 2 , v → ⋅ w → = - 4 , e a n gu → ,v → = π / 3 , calcule: 5 u → - w → ⋅ ( w → - 2 u → )
Calcule 2 u → + 4 v → 2 , sabendo que u → é unitário, v → = 2 , e a medida angular entre u → e v → é 2 π / 3 radianos.