Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 77
Como deve ser escolhido o ponto sobre o segmento de forma a maximizar o ângulo ?
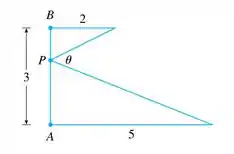
Passo 1
E aí, galerinha! 😎
Nesse problema temos que determinar o ponto sobre o segmento de forma a maximizar o ângulo na figura do enunciado.
Parece complicado? 😇
Precisamos preencher a figura que nos foi dada com outras informações para conseguirmos visualizar melhor:
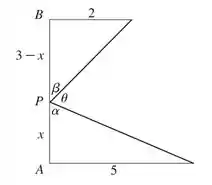
Para resolver essa questão, temos que encontrar uma função para que dependa de uma única variável e então derivar e igualar a zero.
Veja só! 😐
Passo 2
O que o exercício pede é o valor máximo de , então temos que colocá-lo em alguma fórmula, fazer ele depender de apenas uma variável e pronto, a gente pode maximizá-lo. Conseguimos colocar em:
Precisamos isolar e , de forma a escreve-los dependendo da mesma variável.
Para isso, vou usar que a tangente de é dada por
E a tangente de é dada por
Agora sim, ambas dependem do lado .
Substituindo em :
Perfeito né, encontramos uma função para o ângulo que depende de uma única variável
Tranquilo até aqui? 😉
Passo 3
Tendo dependendo de apenas uma variável, vamos maximizá-lo:
Aqui vamos usar a derivada do arco tangente que é:
Além da regra da cadeia.
Nossa função é:
Derivando temos:
Igualando a zero, temos:
Vamos agora multiplicar cruzado:
Tá sentindo esse cheirinho de equação de segundo grau.Resolvendo por Bhaskara temos:
Como tem que variar entre e , que é o tamanho de , a única raiz possível é
, então, a posição de que maximiza é:
E aí! entendeu tudo? Responde Aí! 😊
Resposta
A posição de que maximiza é: