Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.11 - Ex. 52
O diâmetro de uma árvore era de 10 polegadas. No ano seguinte, a circunferência aumentou 2 polegadas. Qual foi a variação aproximada do diâmetro da árvore? E da área da seção transversal?
Passo 1
- Variação do diâmetro:
- Variação da área da seção transversal:
Temos que a variação de uma função é dada por: , em que é o valor inicial da variável e é a variação da variável.
Sabemos que o comprimento da circunferência é dada por: .
E que o diâmetro é o dobro do raio, certo? Vamos substituir o r na nossa fórmula então por ...
A variação da circunferência então é dada por: , em que é a variação da circunferência e é a variação do diâmetro.
Ótimo! Agora só temos que perceber qual variação queremos. Perceba que o enunciado nos deu a variação da circunferência (2 p) , e nos pediu a variação do diâmetro.
Então:
Que é a variação aproximada do diâmetro.
Passo 2
Primeiramente, o tronco da árvore tem o formato de um cilindro, logo queremos a área da seção transversal do cilindro. Mas o que é seção transversal? Bom, no cilindro é a interseção do cilindro com um plano paralelo à base. Assim:
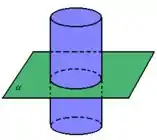
Então, o que temos que fazer é calcular a variação da área do círculo com diâmetro inicial de 10 polegadas e com uma variação de 2 polegadas depois.
Usando o mesmo raciocínio do item anterior, temos:
Que é a variação da área da seção transversal.
Resposta
e .