Exercícios de Diferencial – Valor Relativo - Lista de Exercícios Resolvida

Uma menina muito curiosa resolveu calcular a área superficial e o volume de uma corda bem grossa. Sabendo que a corda tinha comprimento suficiente, e exato, para envolver um bambolê de de raio e que a corda tinha raio exato de . O erro possível de cálculo do raio da corda é de Estime:

1. O erro e o erro percentual do cálculo da área superficial da corda
2. O erro e o erro percentual do cálculo do volume da corda

OBS: A menina sabe que, independente de calcular como ela fez esse cálculo, a proporção entre o raio do bambolê e da corda é fixa.

Um professor um pouco pirado entregou pra seus alunos o gráfico da curva e pediu para que calculassem a área abaixo do gráfico entre e . Os alunos optaram por calcular essa área usando um triângulo retângulo cuja hipotenusa tangenciasse a curva. Abaixo, uma representação de como esse triângulo muda em função do ponto de tangência:

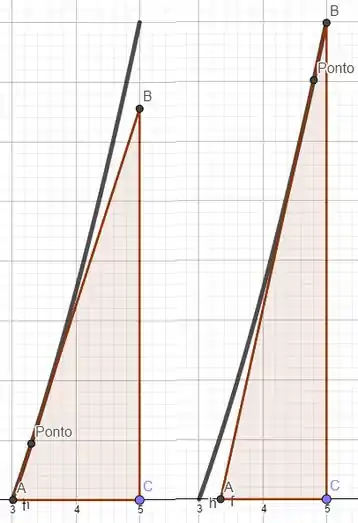
Sabendo que os alunos escolheram como ponto de tangência e que o erro na marcação desse ponto é de calcule o erro percentual no cálculo de . Depois, calcule também o mesmo erro em relação à área real abaixo da curva.

Uma piscina no formato de um trapézio isósceles tem sua área dada pela fórmula . Abaixo, uma representação dessa piscina:

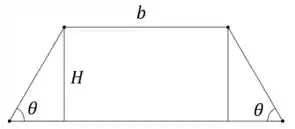
Use diferenciais para aproximar o erro no cálculo de se (exatamente), (exatamente) e com erro possível de .

Além disso, determine o erro percentual no cálculo de .

O lado de um quadrado mede aproximadamente , com erro possível de .

1. Use diferenciais para estimar o erro na área calculada.
2. Estime o erro percentual no lado e na área.

A área de um triângulo retângulo com uma hipotenusa é calculada pela fórmula , onde é um dos ângulos agudos. Use diferenciais para aproximar o erro no cálculo de se (exatamente) e com erro possível de .

Além disso, determine o erro percentual no cálculo de .

A altura e o raio de um cilindro reto são iguais, de modo que o volume desse cilindro é dado por . O volume deve ser calculado com erro não maior que 1% em relação ao valor real. Determine, aproximadamente, o maior erro que pode ser tolerado na medida de , expressando-o como porcentagem de .

Para as funções abaixo, calcule e para os valores de e dados:

Um empresário encomendou de um fabricante de equipamentos de aço uma esfera de raio 12cm. O fabricante entregou-lhe uma esfera com as seguintes informações: “esfera de aço polido com raio ”. Qual a margem aproximadamente de erros do volume e da área da esfera recebida.

Para as funções abaixo, calcule e para os valores de e dados:

Para as funções abaixo, calcule e para os valores de e dados: