Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 72

Dois postes verticais P Q e S T são amarrados por uma corda P R S que vai do topo do primeiro poste para um ponto R no chão entre os postes e então até o topo do segundo poste, como na figura. Mostre que o menor comprimento de tal corda ocorre quando θ 1 = θ 2 .

Passo 1

Fala aí! como vai? 😉

Nesse problema temos dois postes verticais P Q e S T são amarrados por uma corda P R S que vai do topo do primeiro poste para um ponto R no chão entre os postes e então até o topo do segundo poste, como na figura do enunciado.

A partir daí temos que mostrar que o menor comprimento de tal corda ocorre quando θ 1 = θ 2 .

Tem ideia de como fazemos isso? 😐

Vamos dar nome aos bois para facilitar nossa resolução:

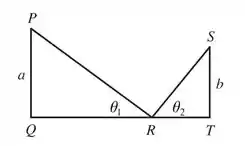
Veja só! 😇

Passo 2

Se d = Q T nós vamos minimizar f θ 1 = P R + R S = a cossec ⁡ θ 1 + b cossec ⁡ θ 2

Derivando com respeito a θ 1 e igualando a zero, nós temos:

d f d θ 1 = 0 = - a cossec ⁡ θ 1 cot ⁡ θ 1 - b cossec ⁡ θ 2 cot ⁡ θ 2 d θ 2 d θ 1

Agora, precisamos encontrar d θ 2 d θ 1   para ser possível resolver nossa derivada, e podemos fazer isso usando Q T = a cot ⁡ θ 1 + b cot ⁡ θ 2 .

Derivando com respeito a θ 1 temos:

d Q T d θ 1 = - a cossec 2 ⁡ θ 1 - b cossec 2 ⁡ θ 2 d θ 2 d θ 1 = 0

d θ 2 d θ 1 =   - a cossec 2 ⁡ θ 1 b cossec 2 ⁡ θ 2

Substituindo em d f d θ 1 :

d f d θ 1 = 0 = - a cossec ⁡ θ 1 cot ⁡ θ 1 - b cossec ⁡ θ 2 cot ⁡ θ 2 - a cossec 2 ⁡ θ 1 b cossec 2 ⁡ θ 2

d f d θ 1 = 0 = - a cossec ⁡ θ 1 cot ⁡ θ 1 + a cossec 2 ⁡ θ 1 cot ⁡ θ 2 cossec ⁡ θ 2

cossec ⁡ θ 2 cot ⁡ θ 1 = cossec ⁡ θ 1 cot ⁡ θ 2

cot ⁡ θ 1 cossec ⁡ θ 1   = cot ⁡ θ 2 cossec ⁡ θ 2

Utilizando propriedades trigonométricas...

cos ⁡ θ 1 = cos ⁡ θ 2

Desde que θ 1   e θ 2 sejam ambos agudos, temos que θ 1 = θ 2 .

E aí! entendeu tudo? Responde Aí! 😉

Resposta

θ 1 = θ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a função densidade de probabilidade normal padrão, determine a probabilidade de que uma escolha ao acaso de x esteja no intervalo [ - 3 ,3 ] . Aproxime o valor da integral definida usandoA regra
Uma cerca de 8 pés de altura corre paralela a um edifício alto, a uma distância de 4 pés do edifício. Qual o comprimento da menor escada que vai atingir do chão, por cima da cerca, à parede do prédio?
Uma mulher em um ponto A na praia de lago circular com raio 2 mi quer chegar no ponto C diametralmente oposto a A do outro lado do lago no menor tempo possível. Ela pode andar a uma taxa de 4 mi/h e r
O gráfico mostra o consumo de combustível c de um carro (medido por galões/hora) como uma função da velocidade v do carro. A baixa velocidade do motor não rende bem; assim, inicialmente c decresce à m
Considere a situação no Exercício 51 se o custo de colocar um cano debaixo do rio for consideravelmente mais alto do que o custo de colocar um cano por terra (US $ 400.000 mil). Você pode suspeitar qu