Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.7 - Ex. 66
Considere a situação no Exercício 51 se o custo de colocar um cano debaixo do rio for consideravelmente mais alto do que o custo de colocar um cano por terra (). Você pode suspeitar que, em alguns casos, a distância mínima possível sob o rio deve ser usada e deve estar localizado a da refinaria, diretamente em frente aos tanques de armazenamento. Mostre que esse nunca é o caso, não importa qual seja o custo "abaixo do rio".
Passo 1
Fala aí! tudo certinho?
Nesse problema temos que voltar na historinha do exercicio 51 mais uma vez para mostrar que o caso de construir o óleoduto a leste até a frente dos tanques e cruzar o rio perpendicularmente nunca será o caminho mais barato.
Parece complicado?
Caso você não se lembre desse exercicio, não se preocupe... temos uma refinaria à margem de um rio que tem de largura. A a leste, do outro lado do rio, ficam os tanques de armazenamento. Nosso objetivo é construir um oleoduto que ligue a refinaria até os tanques.
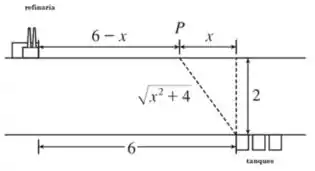
O custo de construção do oleoduto sobre a terra é de e o custo de construção sob o rio é . Vamos reciclar do exercicio 51 a equação que relaciona o custo com a distância e aplicar a metodologia dos pontos críticos (derivando e igualando a ).
Saca só!
Passo 2
A função custo é dada pela distância percorrida à margem multiplicada pelo custo do trecho por terra mais a distância construída sob o rio multiplicada pelo custo do trecho submerso.
A equação do custo , em $100.000, é dada por:
Onde é o custo em de colocar a tubulação sob o rio.
Vamos encontrar o valor crítico de através da primeira derivada da função custo:
Pela regra da cadeia, temos
Tranquilo até aqui?
Passo 3
Igualando a para encontrar o ponto crítico
Elevando os dois lados ao quadrado para simplificar a raiz
Isolando
Como podemos ver, mesmo o preço tendendo a infinito, nunca será exatamente igual a zero. Portando o caminho “reto” nunca será o mais barato.
E aí! o que achou? Responde Aí!