Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.7 - Ex. 50
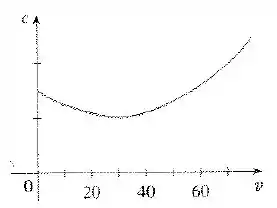
O gráfico mostra o consumo de combustível de um carro (medido por galões/hora) como uma função da velocidade do carro. A baixa velocidade do motor não rende bem; assim, inicialmente decresce à medida que a velocidade cresce. Mas a uma alta velocidade o consumo cresce. Você pode ver que é minimizado para esse carro quando mi/h. Porém, para a eficiência do combustível, o que deve ser minimizado não é o consumo em galões/hora, mas, em vez disso, o consumo de combustível em galões por milha. Vamos chamar esse consumo de . Usando um gráfico, estime a velocidade na qual tem seu valor mínimo.
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão dá pra gente o seguinte gráfico:
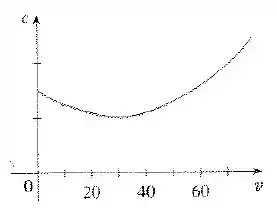
E nos diz que ele mostra o consumo de combustível de um carro (medido por galões/hora) como uma função da velocidade do carro.
Podemos perceber que a baixa velocidade o motor não rende bem; assim, inicialmente decresce à medida que a velocidade cresce. Mas a uma alta velocidade o consumo cresce.
Podemos ver que é minimizado para esse carro quando mi/h.
Mas a questão nos diz que, para a eficiência do combustível, o que deve ser minimizado não é o consumo em galões/hora, mas, em vez disso, o consumo de combustível em galões por milha.
Vamos chamar esse consumo de , e usando um gráfico, precisaremos estimar a velocidade na qual tem seu valor mínimo.
E para isso, devemos traduzir essa informação, para descobrir quantos galões são consumidos por milha para uma velocidade, uma outra função .
Fazendo isso, iremos tentar esboçar um gráfico de , para então encontrar o valor de para o qual é mínimo. lembrando que nesse ponto teremos:
Agora, que já sabemos o que fazendo, vamos colocar a mão na massa. Vem comigo.
Passo 2
Primeiro iremos tentar achar em função de e . Se o veículo viaja a milhas por hora e consome galões por hora, para cada hora ele viaja milhas e consome galões. Temos então:
A função é então composta dessa maneira:
Passo 3
Sabemos que temos um ponto crítico da função quando . Usando a técnica de derivação de razão entre funções, podemos derivar em relação a :
Se :
Podemos isolar , ficando com:
Sabemos que a derivada é a inclinação da reta tangente à curva de num ponto de abcissa . Além disso, é a tangente do ângulo entre a horizontal e uma reta traçada da origem até um ponto da curva. Vamos representar esses dois valores, como exemplo, para a velocidade de 40 mi/h:
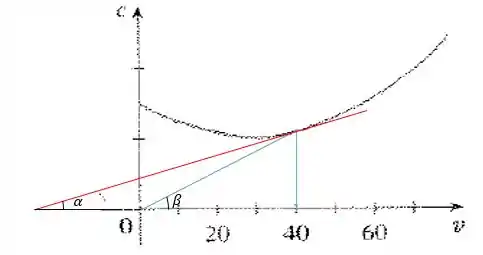
A linha vermelha é tangente à curva no ponto, e a tangente é:
O ângulo representa a divisão de por :
Logo, se as tangentes são iguais para o ponto , a reta tangente à curva nesse ponto deve passar na origem! Podemos colocar uma reta no eixo , e ir girando ela até tocar na curva. Achamos então um valor aproximado de :
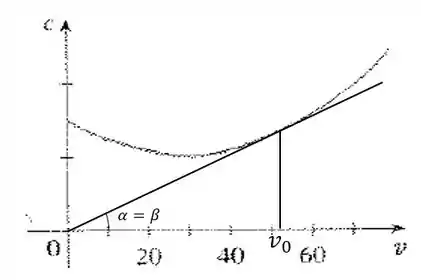
Temos então: