Uma mulher em um ponto na praia de lago circular com raio 2 mi quer chegar no ponto diametralmente oposto a do outro lado do lago no menor tempo possível. Ela pode andar a uma taxa de 4 mi/h e remar um bote a 2 mi/h. Como ela deve proceder?
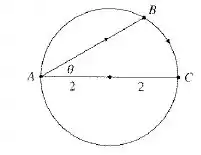
Passo 1
O que queremos fazer aqui é representar o tempo total que leva a mulher até o ponto , dependendo do ângulo de partida dela no lago em relação a . Esse tempo depende da parte que ela vai nadando e da parte que ela rema o bote no interior do lago. Após encontrar , vamos encontrar seu mínimo absoluto para .
Passo 2
Primeiro vamos calcular o tempo que ela leva de até . A velocidade na água é 2 mi/h. Sabemos da física que o tempo é calculado da seguinte maneira:
Sendo a distância em milhas e em horas. Agora calculamos pelo triângulo :
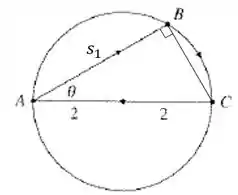
Então temos finalmente o tempo :
Passo 3
Calculamos então o tempo que a mulher leva de até , ao longo da circunferência. A velocidade dela nesse trecho é mi/h. Novamente, temos:
Pela figura a seguir, podemos encontrar o arco em função de :
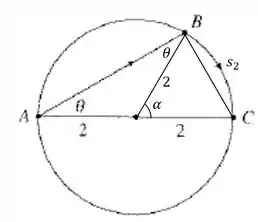
O ângulo é achado facilmente:
Então o cálculo do arco é feito:
Finalmente, temos também o tempo em função de :
Sendo dado em radianos.
Passo 4
Temos então, somando e , o tempo total de viagem da moça de a :
Teremos um ponto crítico quando a derivada for zero ou não existir. Derivando a função:
Como a derivada sempre existe para , vamos ver quando ela se anula:
Passo 5
Agora temos o único ponto crítico, vamos então analisar o valor do tempo nesse ponto e nos extremos e . Temos:
Isso quer dizer que na verdade, o ponto é um máximo da função tempo, de modo que o ponto que minimiza a função ocorre em:
Ou seja, o caminho mais rápido para a moça é quando ela opta por não entrar no lago e remar, apenas caminhar ao redor lago.
Resposta
A mulher deve apenas caminhar ao redor do lago, partindo de um ângulo .