Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 71
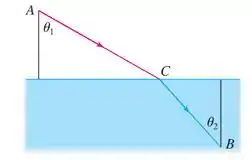
Seja a velocidade da luz no ar e a velocidade da luz na água. De acordo com o Princípio de Fermat, um raio de luz viajará de um ponto no ar para um ponto na água por um caminho que minimiza o tempo gasto. Mostre que
Onde (o ângulo de incidência) e (o ângulo de refração) são conforme mostrados. Essa equação é conhecida como a Lei de Snell.
Passo 1
E aí, pessoal! 😁
Nesse problema temos que mostrar que
Onde a velocidade da luz no ar e a velocidade da luz na água e de acordo com o Princípio de Fermat, um raio de luz viajará de um ponto no ar para um ponto na água por um caminho que minimiza o tempo gasto.
Tem ideia de como fazemos isso? 🤔
Para resolver o exercício vamos esboçar o seguinte desenho, dando nome aos lados que vão auxiliar nossa resolução:
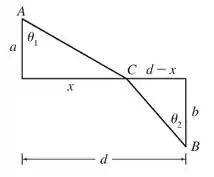
Queremos minimizar o tempo em que um raio de luz leva pra cruzar as retas e , então primeiramente vamos aplicar Pitágoras nos dois triângulos retângulos formados nas figuras para acharmos essas medidas:
Veja só! 😉
Passo 2
A fórmula da velocidade é , então, para encontrarmos o tempo , faremos:
Tranquilo até aqui? 😎
Passo 3
Minimizando :
Isso prova a Lei de Snell.
E aí! entendeu tudo? Responde Aí! 😉
