Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 13
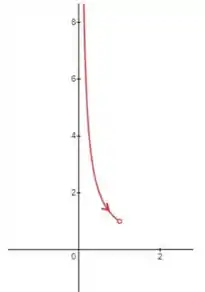
- Elimine o parâmetro para encontrar uma equação cartesiana da curva:
- Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
E aii, vamos ver o que essa questão ta pedindo?
Primeiro, precisamos achar a equação cartesiana da curva... mas o que é isso? É uma equação que relaciona e , e representa a curva!
Pra fazer isso, a gente vai comparar as equações paramétricas de e :
e
Lembrando que a equação cartesiana não pode mais ter o , vai depender só de e !!
Depois, a gente vai precisar esboçar a curva, que vamos fazer a partir da equação cartesiana que acharmos em (a).
A direção e o tamanho da curva dependem do parâmetro que a questão deu:
Ou seja: a curva vai de até
A gente tá falando que o tende pra esses valores porque o parâmetro tá definido em um intervalo aberto (ou seja, os pontos onde e não fazem parte da curva!)
Então vamos colocar a mão da massa!
Passo 2
(a)
Como precisamos comparar com , vamos lembrar da definição de cossecante:
Assim, podemos dizer que
Já que
E pronto! Nossa equação cartesiana fica:
Porém, o intervalo de parametrização é
Portanto não estamos falando da curva inteira, apenas de uma parte dela.
Para encontrar que parte é essa vamos calcular os limites do intervalo de definição de :
Se temos
Se temos
Ou seja
E
Então, a equação cartesiana da curva é
Passo 3
(b)
Para esboçar a curva, primeiro vamos lembrar qual é o formato do gráfico de
Esse gráfico é uma hipérbole e tem o seguinte formato:
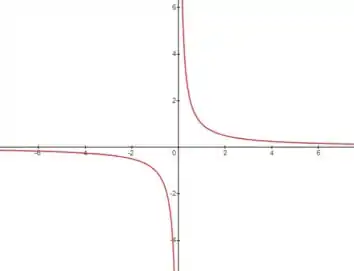
Os limites de definição da curva a gente já achou:
Falta só encontrar a direção que a curva é traçada conforme aumentamos o valor de .
A gente calculou dos limites do intervalo o seguinte:
Ou seja, conforme aumentamos o valor de , o valor de está aumentando e o de diminuindo.
Com isso já conseguimos traçar a curva:
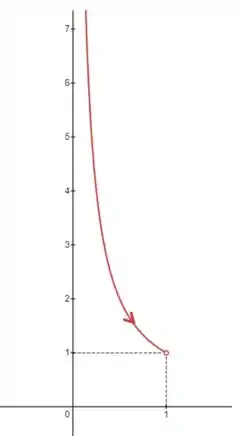
Algumas coisas importantes sobre esse gráfico:
- Percebeu que o ponto tá com uma bolinha aberta? Isso porque esse é o ponto quando , e a curva tá definida só pra , então esse ponto não faz parte da curva!
- A seta que mostra a direção da curva tá seguindo na direção desse ponto , que é a direção que o parâmetro está crescendo.
Resposta
