Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.Revisão - Ex. 10
Esboce a curva polar.
Passo 1
Eaee, belezinha?? Bom... queremos plotar a seguinte equação polar:
Para isso, vamos primeiro plotar essa curva no plano cartesiano para observarmos as principais características da curva.
Mas pra que isso??
Porque assim fica mais fácil de a gente plotar no plano polar pos observamos os quadrantes bem direitinho 😉
Mas e para plotar no plano cartesiano??
Basta comparar com uma função conhecida 😉
Passo 2
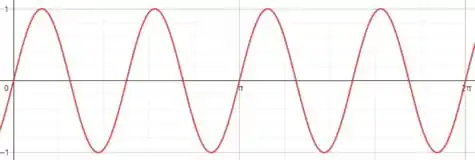
Bom... Sabemos que uma função parecida com é
Que é dada assim:
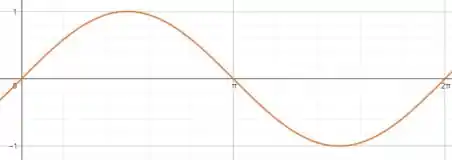
Perceba que a única diferença entre as duas funções é que na do enunciado temos um multiplicando.
Esse multiplicando significa que a nossa curva está sendo “comprimida” numa razão de vezes a curva do seno.
Assim, temos:
Passo 3
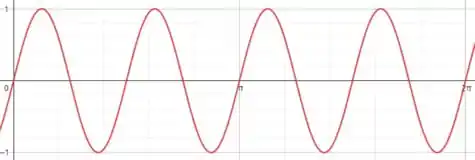
Perceba que a nossa curva se repete a cade .
Isso significa dizer que basta analisarmos apenas o o que acontece no intervalo e aí a gente repete a nossa análise para os demais!!
Bom... se analisarmos o intervalo , percebemos que no plano polar teremos dois “laços” com a seguinte forma:
Assim, aplicando ao intervalo completo , vamos ter a seguinte curva:
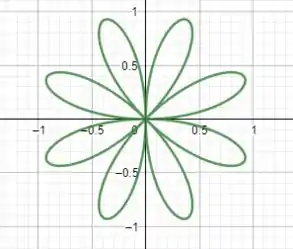
Aqui também vale ressaltar que o intervalo do parâmetro é . Intervalos menores não completam a curva e intervalos maiores não fazem diferença para a plotagem!
Resposta
