Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 17
- Elimine o parâmetro para encontrar uma equação cartesiana da curva:
- Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Faala, tudo certo?!
Vamos entender o que a questão tá pedindo:
Na letra (a) ela quer que elimine o parâmetro (que é o ) pra encontrar uma equação cartesiana. A gente vai querer comparar as equações paramétricas:
E achar uma forma de relacionar e sem depender de .
A gente vai precisar lembrar de algumas coisas de funções hiperbólicas. Primeiro, essas funções são definidas assim:
E para qualquer valor de :
Na letra (b), a gente vai precisar traçar a curva (usando essa equação que encontramos em (a)) e indicar a direção que a curva segue conforme o valor de aumenta.
Já que a questão não deu limites pro parâmetro, uma boa forma da gente saber a direção é testando valores de , e perceber pra onde a função está andando quando eu aumento esse valor!
Passo 2
(a)
Para “isolar” o parâmetro no caso em que temos seno hiperbólico e cosseno hiperbólico, usamos a relação:
Como isso vale pra qualquer valor de , a gente pode simplesmente reescrever:
Assim
Essa equação que achamos é a equação de uma hipérbole, “olhando” para o eixo , que é a variável que tá com sinal negativo.
Além disso, como
Vale para qualquer valor de , podemos escrever:
Então, a equação cartesiana que descreve a curva é:
Passo 3
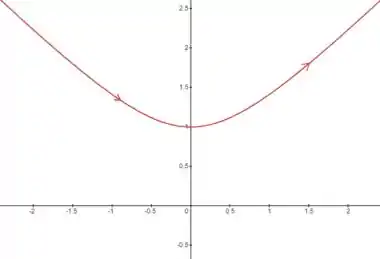
(b)
A gente já sabe que a curva que vamos esboçar é uma hipérbole, mas ela está limitada para .
Assim, estamos falando do ramo da hipérbole que está na parte positiva do eixo , com foco no ponto .
Traçando nossa curva, temos
Para saber a direção que a curva é traçada, vamos calcular o valor de para , e :
Para :
Vamos reescrever como , e fazer a subtração de frações no numerador:
Da pra saber que isso é menor que zero, porque , então .
Para :
Para :
Que é maior que zero, já que .
Agora vamos marcar esses pontos no gráfico:
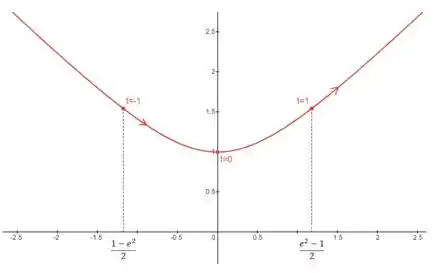
Percebeu que conforme aumentamos o valor de , os pontos estão andando “pra direita”? Essa é a direção que a curva é traçada, que indicamos com as setas!
Resposta
