Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 41
Encontre todos os pontos de interseção das curvas dadas
Passo 1
Quer dizer então que precisamos encontrar os pontos de interseção das duas curvas.
Temos as curvas:
E para encontrarmos os pontos de interseção, deveremos igualar as equações dessas curvas, encontrarmos os ângulos em que elas se encontram, e após isso poderemos encontrar o raio que isso acontece substituindo o ângulo encontrado em qualquer uma das duas equações.
Mas também deveremos testar se as curvas de encontram na origem. Isso é, deveremos fazer , se existe qualquer valor de que satisfaça isso, quer dizer que nossas funções se encontram na origem, independente para qual valor de de cada uma.
Passo 2
Vamos buscar esses pontos.
Igualando as curvas:
Aplicando a forma do seno do arco duplo:
E daí, temos que
Ou
Olhando o círculo trigonométrico:
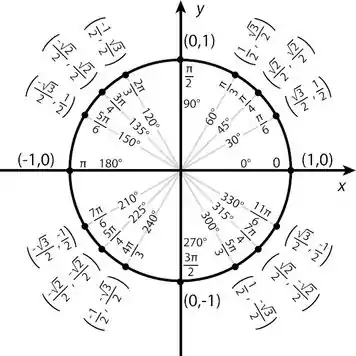
Temos então que:
E
Passo 3
Agora que já encontramos os valores de para os quais as duas curvas se intersectam, vamos encontrar o valor de também?
Assim a gente forma o ponto bonitinho e fecha logo a questão!
Para isso, é só substituir os valores de em uma das curvas, já que como é um ponto de inteseção, tanto faz a curva que vamos escolher, as duas vão dar o mesmo ponto!
Para :
Veja que nem precisamos testar se as figuras se encontram na origem, por termos as funções seno aqui, e que possuem um que a zeram.
Para :
Para :
Os pontos de interseção são, portanto,