Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.11 - Ex. 61

Encontrar a área da região delimitada pelo laço interno da limaçon r = 1 + 2 s e n   θ .

Passo 1

(Não desespere com esse nome aí haha...)

A área pedida está na figura:

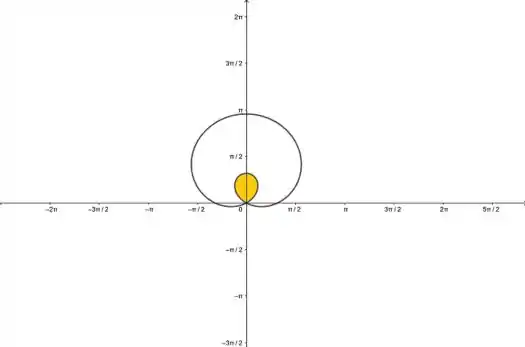
Passo 2

A gente usa a fórmula:

A = 1 2 ∫ α β f θ 2 d θ  

O intervalo dessa área vai de 7 π 6 , 3 π 2 . Então bora lá...

A = 1 2 ∫ 7 π 6 3 π 2 1 + 2 s e n   θ 2 d θ

A = 1 2 ∫ 7 π 6 3 π 2 1 + 4 s e n   θ + 4   s e n 2 θ   d θ

= 1 2 θ - 4 cos ⁡ θ + 4 θ 2 - s e n   2 θ 7 π 6 3 π 2

= π - 3 3 2 u . a

Prontinho! Essa é a área que pediram😉

Resposta

π - 3 3 2 u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercicios de 1 a 36, faça um esboço do gráfico da equação dada 2. (a) θ = 3 4 π ; br = 3 4 π
Nos Exercíccios de 1 a 36, faça um esboço do gráfico da equação dada. 4. (a) θ =- 3 ; b r = - 3
Nos Exercicios de 1 a 36, faça um esboço do gráfico da equação dada 8. (a)r c o s θ =- 5 ; br - 5 c o s θ
Nos Exercícios de 1 a 36; faça um esboço do gráfico da equação dada 6. (a) r s e n θ = 2 ; b r = 2 s e n θ
Nos Exercicios de 1 a 36, faça um esboço do gráfico da equação dada 3. a θ = 2 ; b r = 2