Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.7 - Ex. 28
Encontre a área do maior retângulo que pode ser inscrito em um triângulo retângulo com catetos de comprimento e cm, se dois dos lados do retângulo estiverem sobre os catetos.
Passo 1
Falai galerinha, tudo certo:
Como diria a Viúva Negra, “Ainda somos amigos, certo?”
Boraaa fazer essa comigo
O enunciado pediu pra gente encontrar a área do maior retângulo que pode ser inscrito em um triângulo retângulo, sabendo que esse triângulo tem catetos de comprimento e e que os dois lados do retângulo estão sobre os catetos.
Esboçando isso, temos a seguinte figura:
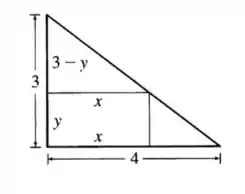
Para um triângulo retângulo com catetos o maior retângulo inscrito, com dois lados sobre os catetos, tem uma área máxima quando suas dimensões são metade dos catetos do triângulo.
Isso ocorre porque o retângulo formará outro triângulo semelhante dentro do triângulo original, e podemos usar proporções para calcular a área máxima.
Vamos usar a fórmula para a área de um retângulo:
Vamos determinar a função área em termos de uma variável para maximizar usando cálculo.
Vamos lá!
Passo 2
Primeiro, visualizamos o triângulo retângulo com os catetos 3 cm e 4 cm, e a hipotenusa será dada pelo Teorema de Pitágoras:
Aqui,
Então, a hipotenusa será:
Agora, precisamos encontrar o maior retângulo que pode ser inscrito nesse triângulo, com dois de seus lados sobre os catetos do triângulo. Para isso, devemos maximizar a área desse retângulo.
Passo 3
Consideremos como a largura do retângulo ao longo do cateto de como a altura ao longo do cateto de
Devido à semelhança dos triângulos, a razão entre os catetos do triângulo retângulo formado dentro do triângulo original deve ser igual:
Isso vem da soma das proporções de em relação aos catetos totais do triângulo.
Passo 4
Escrever a relação:
Isolar em função de
Expressar a área do retângulo em função de
Passo 5
Então, o que a gente vai fazer é maximizar a área do retângulo, , relacionando essas variáveis através da semelhança de triângulos e encontrando os pontos críticos da equação, por meio da derivada.
Derivar a função área em relação a para encontrar o ponto de máximo:
Encontrar o ponto crítico definindo a derivada igual a zero:
Calcular correspondente a
Passo 6
Calcular a área máxima do retângulo:
Portanto, a área do maior retângulo que pode ser inscrito no triângulo retângulo com catetos de
“Nós somos Groot”
Resposta
Portanto, a área do maior retângulo que pode ser inscrito no triângulo retângulo com catetos de