Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.4 - Ex. 27
Encontre a área do paralelogramo com os vértices , , e .
Passo 1
Bom galera, gente tem os vetores:
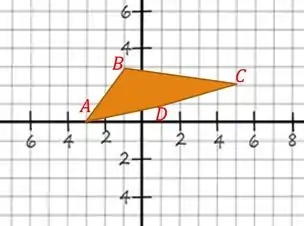
Vamos começar desenhando esse paralelogramo para ajudar:
Passo 2
Beleza, por definição para calcular essa área a formula é:
Onde e são os determinantes de matrizes, elas são:
Se quiser saber mais sobre isso, é só assistir aulas aqui mesmo no Responde aí, dá uma olhadinha lá!
Passo 3
Então, vamos calcular os determinantes:
Passo 4
E pra terminar, tá fácil agora, é só botar naquela fórmula lá:
Resposta
Exercícios de Livros Relacionados
Calcule a área do triângulo A B C , sendo A B → = ( - 1 ,1 ,0 ) e A C → = ( 0 ,1 ,3 ) .
O triângulo A B C tem área 4 . Sabendo que B = A + u → e C = A + v → , calcule u → ∧ v → .
A medida angular entre u → e v → é 30 ° , e suas normas, 2 e 3 . Calcule u → ∧ v → .
Sabendo que u → = 1 e v → = 7 e a n gu → ,v → = π / 6 , calcule u → ∧ v → e 4 u → ∧ 9 v → .
Demonstre e interprete geometricamente as relações:a) u → ∧ v → ≤ u → v → b) u → ∧ v → = u → v → ⇔ u → ⊥ v →