Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 11.Exercício - Ex. 19
Calcule a área do triângulo , sendo e .
Passo 1
O problema pede para calcularmos a área do triângulo formado pelos vetores e .
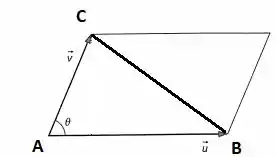
Sabemos que a área do paralelogramo é dada pela norma do produto vetorial, de modo que a a´rea do triângulo será metade:
Passo 2
Usando a fórmula do produto vetorial com determinante:
Calculando a norma:
Resposta
Exercícios de Livros Relacionados
Determinar um vetor unitário simultaneamente ortogonal aos vetores v 1 → = ( 1 ,1 ,0 ) e v 2 → = ( 2 ,- 1 ,3 ) . Nas mesmas condições determinar um vetor de módulo 5.
Determinar v → tal que v → seja ortogonal ao eixo y e u → = v → × w → , sendo u → = ( 1 ,1 , - 1 ) e w → = ( 2 ,1 ,1 ) .
Sendo os vetores u → e v → vetores do espaço, com v → ≠ 0 :Determinar o número real r tal que u → - r v → seja ortogonal a v → ;
Calcular a área do paralelogramo que tem um vértice no ponto A ( 3 ,2 ,1 ) e uma diagonal de extremidades B ( 1 ,1 , - 1 ) e C ( 0 ,1 ,2 ) .
Dados os vetores a → = ( 3 ,4 ,2 ) e b → = ( 2 ,1 ,1 ) , obter um vetor de módulo 3 que seja ao mesmo tempo ortogonal aos vetores 2 a → - b → e a → + b → .