Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.9 - Ex. 27

Encontre a área da região delimitada pelos gráficos de y = 1 1 - 9 x 2 ,   y = 0 ,   x = 0   e   x = 1 6 .

Passo 1

Antes de escrevermos a integral que temos que resolver, vamos esboçar essa região, se liga:

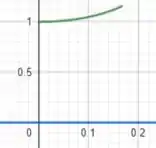
Ou seja, queremos encontrar quanto vale a área da região abaixo dessa curva verde, que vai de 0 até 1 6 . Sendo assim, a integral que temos que resolver é:

∫ 0 1 6 1 1 - 9 x 2 d x = ∫ 0 1 6 1 1 - 3 x 2 d x

Passo 2

Para resolver essa integral vamos utilizar a seguinte substituição:

u = 3 x

Disso tiramos que:

d u = 3 d x

∴ d u 3 = d x

Substituindo na nossa integral:

∫ 0 1 6 1 1 - 3 x 2 d x = 1 3 ∫ 0 1 6 d u 1 - u 2

Resolvendo:

1 3 ∫ 0 1 6 d u 1 - u 2 = 1 3 a r c   s e n   u 1 6 0 = 1 3 a r c   s e n   3 x 1 6 0

∴ ∫ 0 1 6 1 1 - 3 x 2 d x = π 18   u . a

E esse é o valor da nossa área, galera!

Resposta

Área: π 18   u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

31-50. Calcule as integrais por qualquer método.40. ∫ π 2 4 π 2 1 x . s e nx d x
31-50. Calcule as integrais por qualquer método.39. ∫ 0 π 5 x . cos ⁡ x 2 d x
19-22. Calcule a integral definida expressando-a em termos de u e calculando a integral resultante usando uma fórmula de Geometria.21. ∫ π 3 π 2 s e nθ 1 - 4 c o s 2 θ d θ ; u = 2 cos ⁡ θ
31-50. Calcule as integrais por qualquer método.48. ∫ 1 2 1 x . 4 - x d x
19-22. Calcule a integral definida expressando-a em termos de u e calculando a integral resultante usando uma fórmula de Geometria.22. ∫ e - 3 e 3 9 - ln ⁡ x 2 x d x ; u = ln ⁡ x