Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.1 - Ex. 5b
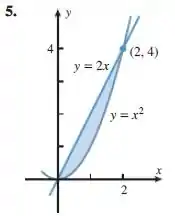
Encontre a área da região sombreada integrando em relação a y:
Passo 1
Para calcularmos a área entre as curvas vamos calcular a integral fazendo a diferença entre as funções de cima e debaixo, no entanto, nesse caso, queremos em relação a y vamos escrever a integral em função a y, lembrando que y varia entre 0 e 4.
Nosso primeiro passo será então isolar o x em cada função.
Nossa integral ficará então:
Passo 2
Calculando isso temos:
Resposta
Exercícios de Livros Relacionados
Determine as áreas das regiões compreendidas entre as retas e as curvas y = 7 - 2 x 2 E y = x 2 + 4
Determine as áreas das regiões compreendidas entre as retas e as curvas y = x 2 - 2 x E y = x
Determine as áreas das regiões compreendidas entre as retas e as curvas y = x 2 E y = - x 2 + 4 x
Desenhe a curva dada (coordenadas polares ). d )ρ = 2
Desenhe a curva dada (coordenadas polares ). b ) ρ cos θ = 1 , - π 2θπ 2