Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 1c
Desenhe a curva dada (coordenadas polares ).
Passo 1
Nesse caso acontece algo particularmente estranho, quando isolamos o ocorre que teremos:
Sabemos que , ou seja, ele varia entre esse valores, o que, se jogarmos os valores na equação, teremos nos dois extremos.
Vamos montar a tabela e ver o que acontece
Passo 2
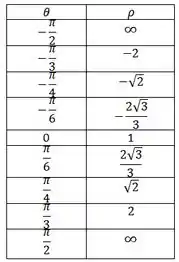
Parece não ter nada de mais nesses valores, mas se vc colocar esse valores em um triângulo com entre e a base e a hipotenusa, e fizer o valor de como sendo o valor da hipotenusa, você vai perceber que todos os valores para o tamanho da base dão 1.
Isso se dá por que quando calculamos a
Quando igualamos a nossa relação achamos que , ou seja, independente do valor de sempre vamos encontrar um ponto que está na mesma linha do semi-eixo 0x.
Passo 3
Assim nosso gráfico fica:
Resposta
