Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.1 - Ex. 1

Encontre a área da região sombreada:

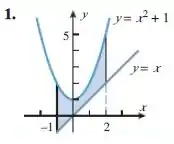
Passo 1

Para calcularmos a área entre as curvas vamos calcular a integral fazendo a diferença entre as funções.

int_(- 1)^2 x^2 + 1 - x d x

Passo 2

Calculando isso temos:

(x^3)/(3) + x - (x^2)/(2) | [[2],[-,1]]

(8)/(3) + 2 - 2 + (1)/(3) + 1 + (1)/(2) = (9)/(2)

Resposta

(9)/(2)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Questão: 35 Ache a área da região limitada pela curva y = ln ⁡ x , pelo eixo x e pela reta x = e ² ².
Questão: 39 Ache a área da região limitada pela curva y = 2 x e - x 2 , pelo eixo x e pela reta x = 4 .
Questão: 42Ache o centroide da região limitada pela curva y = e x , pelos eixos coordenados e pela reta x = 3 .
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada.A região limitada pela parábola x = y 2 - y e pela reta y = x .
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada.A região limitada pelo eixo y e pela curva x = y - y 3 , 0 ≤ y ≤ 1 .